/* cospan-composition */
インスティチューション(institution)(*注1)の定義の一部として、指標 (signature)Σに対する文(sentence)の集合Sen(Σ)が登場する。Senは、 指標圏Signから集合の圏Setへの共変関手Sen:Sign→Setである。指標圏Signに 一定の条件を課した上で、関手Senを利用して、“圏Sign上のセオリーの圏” を構成する。
インスティチューションは、(僕は読んでないけど)Joseph Goguen & Rod Burstall "Institutions: Abstract model theory for specification and programming" (1992) で導入された概念。 Goguen自身による 紹介 institutions がある。どうでもいいことだが、Goguen先生 の奥様(Ryoko Goguen) は日本人らしい。The Tatami ProjectのTatamiは「畳」なのか? 2003年来日のときのご夫妻の写真が ココにあります。
Senを使わずにセオリーの圏をもっと直接的に定義するほうが望ましいだろう が、今回は話題にしない。また、 モデル関手Modは、Sign上に定義するのではなくて、 セオリーの圏Theory(Sign)に対して定義すべきだと思われるが、Modの定義も 別の機会にゆずる。
Signは有限余完備だとする。つまり、Sign内の任意の有限図式D(*注2)に対 して余極限colim Dが存在すると仮定する。特に、Signの任意の 対象A, B(*注3)に対して、直和 A + B、直和の単位(かつ始対象)0が存在する。 Signの具体例としては、対象Aがなんらかの集合として表現され、射が集合間 の単射であるような圏を想定するとよい。
C内の図式とは、有向グラフδから、有向グラフと見なしたCへのグラフ写像 D:δ→C のことである。その余極限は、Cの対象Xと、 δの頂点で添字付けられたCの射の族{fa:D(a)→X | a∈|δ| }で(余)普遍 性条件を満たすものである。
指標圏の対象はΣ、Γなどと書く習慣だが、ここでは、A, Bなどを使う。
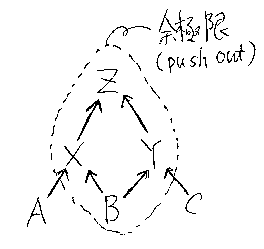
Sign内の図式 (A←X→B)をスパン(span)、図式 (A→X←B)を余スパン (cospan)と呼ぶ。Signの余スパンを射とする圏Cospan(Sign)を構成できる(*注4)。 その構成法の概略を以下に示す。
スパン/余スパンの圏の構成には、微妙な問題がある。実際には、スパンの 結合はup to isoでしか決まらないので、適当な同値関係を入れないと、普通 の意味の圏にはならない。
記述の簡略化のためにCospan(Sign)をCと書く。
/* cospan-composition */

関手Senをもう少し精密化しておく。A∈|Sign|に対するSen(A)は単なる集合では なくて、閉包演算子(closure operator)(*注5)が定義されているとする。閉 包演算子を持つ集合を‘閉包空間’と呼ぶことにして、閉包演算子を保つ写像 を射と考え、その圏をCloSとしておく。すると、SenはSign→CloSという関手 である。
(-)- はPow(X)上で定義された演算子(自己写像)で、A⊆X に対して、 A⊆BならA- ⊆ B- (単調)、 A⊆A- (増大的)、(A-)- = A- (べき等)だとする。
実際には、閉包演算子(-)-は演繹に対応する。S⊆Sen(A)に対して、 S-は公理系Aから(なんらかの演繹系で)導出される定理の全体である。が、 とりあえず具体的な演繹系は考えない。
A∈|Sign|に対して、‘指標Aのセオリー’(theory)とは、Sen(A)の部分集合 のことである(セオリーは公理系といっても同じことである)。指標Aのセオ リーの全体は、(Powはベキ集合を表すとして)Pow(Sen(A))である。これを Theo(A)と書いて、自然に共変関手に拡張する。すると、TheoはSignから閉包 付き束(lattice with closure operator)の圏Latt-Colへの共変関手となる。
セオリーを射とするような圏を定義しよう。有限余完備な指標圏Signから、 そのセオリーの圏Theory(Sign)を次のように構成する。
記述の簡略化のためにTheory(Sign)をTと書く。
この結合演算が結合的、単位的なのは定義と余スパン/束の性質から出る。
/* theory-composition */
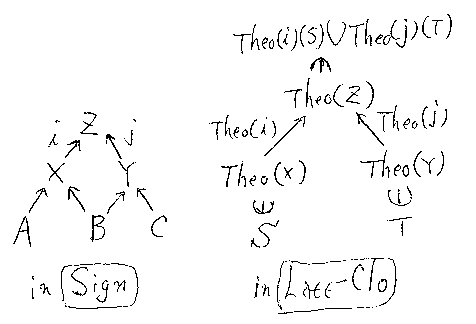
余スパンの圏Cospan(Sign)は単なる圏ではなくて、圏でenrichされている。 よって、二圏(厳密なケース)または双圏(ゆるいケース)によって定式化さ れる。セオリーの集合Therory(Sign)(A, B)はhom圏Cospan(Sign)(A, B)の上の ファイバリング構造を与えることができる。つまり、A, Bを固定して局所的に 考えれば、Theory→Cospanはファイバー圏となる。Therory(Sign)(A, B)に圏 構造を与えることができるので、Theory(Sign)も圏でenrichされている。 Theory(Sign)はなんらかの同境的構造を持つと予想される。
Cospan(Sign)は、Signの直和から導かれるモノイド構造を持つから、対称モ ノイド圏である。このモノイド構造をTheoryまで持ち上げて、さらにトレース を定義できないだろうか? また、|Sign|に極性を追加して、その上にコンパ クト閉圏を作れないだろうか?
Theo(A)は閉包演算を備えた束である。S- = T- で同値関係を入れれば、 閉セオリーだけを考えるのと同じである。Theory(Sign)とClosedTheory(Sign) は圏同値だろう。ClosedTheory(Sign)は、何か幾何学的な圏でenrichされそう な気がする。なぜなら、closed theoryはイデアルのようなものであり、極大 なセオリーは極大イデアルに対応する。そして、極大イデアルは点だと思える からである。
指標圏、セオリー圏の具体的な事例は、Janusコンポネントを射とする圏に対 する仕様の圏である。この具体例で、上記の妄想のどこまでが現実かを確かめ てみたい。