/* system-with-boundary */
現状の形式言語理論に対する“違和感”について述べる。その違和感を解消 するための再定式化(代替案)のラフ・スケッチ(極めてラフ)も述べる。
この記事は、現状の形式言語理論に“ケチをつける”ために書かれている。 まず、僕が「形式言語理論」という言葉で何を指すのかを明確にするために、 この分野の教科書を紹介する(第2節)。それらの教科書に書かれ ている内容には実際にお世話になっている。ケチをつけるどころか感謝すべき ではないか? うん、形式言語理論の成果や効能は十分に認めてますよ。 では、僕が何に不満を感じているのかというと、その定式化(理論構成の筋書 き)がイヤなのだ。基本的/初等的な結果(定理)も、納得がいかないのだ。 「それは、おまえの頭が悪いんだろう」と言われてしまえば、そのとおりでは あるのだが、僕でも分かるような定式化はないものだろうか、という問題意識 も生まれる。
それで僕は、形式言語理論の諸結果が(少なくとも僕にとって)もっと自 然に見える定式化を探すことにした。で、だいたい納得できる形になってきた ので、それを書き記したい。とはいっても、この記事で書くわけではない(別 なシリーズ記事になる予定)。この記事では、僕にとって特に違和感があった “基本的/初等的な結果”について述べる(第4節)。第4節で使 う概念と言葉は、前もって 第3節で説明する。けど、これでセルフ・コンテインドになってい るわけでもないので、第2節で紹介する教科書などを適宜参照していただきた い。
第4節で述べる違和感(すごく気持ちが悪い感覚)が、形式言語理論の再定式 化(あるいはオルタナティブ)を考える動機のひとつだった。もうひとつのキッ カケは、Mark William Hopkinsという人が2001年にUSENETに投稿した 記事 (http://www.lns.cornell.edu/spr/2001-09/msg0035445.html、 http://mathforum.org/epigone/sci.math.research/smimjimpsker/8tt0p9$igu$1@uwm.edu にアーカイブされている)だ(*注1)。彼は、なんと「場の量子論(物理)と 形式言語理論(コンピューティング・サイエンス)のあいだに対応関係がある」 と言うのである。
他にも動機はあるが、今ここでは書かない。いずれ述べる機会があるだろう。
僕は、M.W. Hopkinsの指摘をマジメに考えることにした。だが、物理がまっ たく苦手な僕は、M.W. Hopkinsが示唆していることが正確には理解できない。 物理を勉強する気にもなれないでウダウダしているうちに、位相的場の量子論 のアティヤの公理や、アブラムスキーなどの量子計算に関する定式化 (compact closed categories)が使えそうなことに気が付いた。ここいらの 経緯を第5節に書く。 が、第5節は、個人的なブレイン・ダンプ・メモみたいなものだから、今読ん で理解できるシロモノではないかもしれない。(これから書かれる予定の)形 式言語理論のオルタナティブな定式化の説明を読んだ後でもう一度読んでいた だくとよいだろう。
まず、形式言語理論の教科書を紹介しておこう。よく引き合いに出される定 番といえば、ホップクロフトとウルマンの『言語理論とオートマトン』(ある いは、より新しい『オートマトン 言語理論 計算論』)だ。ホップクロフト/ ウルマンの本(サイエンス社から翻訳が出ている)は確かに名著なんだろうが、 いかにも正統派教科書っぽくて、僕の性には合わない。僕のお気に入りは次の 2冊(*注2)。
僕の本棚には、岩波講座・情報科学6の福村/稲垣 『オートマトン・形式言 語理論と計算論』(岩波書店, 1982)とか、V.J. Rayward-Smith、井上(監修)、 吉田/石丸(訳) 『コンピュータ・サイエンスのための言語理論入門』(共 立出版, 1986)なんてのもあるが、古すぎて入手できないでしょうね。
どちらかをざっと読めば、形式言語理論の予備知識としては十分だろう。基 本的な項目については、どちらにもちゃんとした説明がある。また、それぞれ の著者の価値観により選ばれた特徴的な話題が含まれる。守屋本は、とにかく 題材が豊富で、Kleene代数、ω正規集合、木オートマトンなどにも触れられて いる。有川本ではEFSや拡張遷移ネットワークの話題が面白い。
次の第4節で必要となる概念を、ここでざっと説明しておく。以下で、「言語」 とは、適当なアルファベット上の列言語のことである。特に正規言語を考える。 言語(と呼ばれる集合)のメンバーは列または語(word)と呼ぶ。
正規言語の定義はいろいろあるが、右(みぎ)線形文法による定義が基本的 だ。‘右線形文法’とは、A、Bを非終端記号(AとBが同じでもよい)、αを終 端記号からなる列(αは空列でもよい)として、生成規則が次のどちらかの形 をしている文法だ。
さて、左(ひだり)線形文法という文法もある。まー、たぶん想像はつくだ ろうが、生成規則が次のどちらかの形をしている文法が‘左線形文法’である。
非終端記号が右端にあれば右線形、左端にあれば左線形、わかりやすいね。
もうひとつ、列言語に関する基本概念を説明する -- 列と言語の反転という 概念である。α=a1a2...anを長さがnの列とする。この並び順をひっく り返したan...a2a1をαRと記し、‘反転’と呼ぶ。右肩のRはreverse のつもりである。次のような性質がある。
言語Lの反転LRは次のように定義する: LR={αR|α∈L}。つまり、 Lに属する語の反転をすべて集めた集合がLRである。
右線形文法で生成される言語は、左線形文法でも生成できる。だから、「左 線形文法で生成される言語が正規言語」と定義してもよい。この事実(定理) は、もちろん、先に紹介した教科書にちゃんと書いてある。だが僕は、右線形 文法と左線形文法が生成能力の観点から同値である(同じ言語族を生成する) ことがどうも納得できなかった。教科書の説明や証明を読めば、確かにそうな のだと一応の確認は取れるのだが、釈然としないのである。
右線形規則を使えば、列は右に伸びていく。左線形なら左に伸びていく。だ から、右線形文法で生成された言語を鏡に映したような言語が左線形文法から 生成されるはずである。「鏡に映したような」とは、つまり反転言語ってこと になる。実際、Lが正規言語ならLRも正規言語となるので、全体としてはツ ジツマがあう。だが、やっぱり釈然としない。
この「釈然としない感じ」はどこから来るかというと、対称性が見えないも どかしさである。右と左とか鏡像というのは、対称性である。なのに、説明や 証明から対称性が感じられないのである。
さらにもうひとつ。正規言語に関しては、線形文法と有限オートマトンが対 応関係にあることはよく知られている。文法は生成系であり、かたやオートマ トンは認識系である。お互いに逆の働きを持つ。ここにも対称性、あるいは双 対性がある。だがどうも、生成/認識の対称性が一瞬で見て取れるような構成 にはなっていない。
要するに、現象側には対称性や双対性があるのに、定式化ではそれが隠れて しまっている印象があるのだ。せっかく美しい構造があるのだから、それが明 白に(あるいは露骨に)現れるような定式化がしたいのだ。
「右線形文法と左線形文法が同値」「Lが正規言語ならLRも正規言語」 「文法とオートマトンに対応関係がある」などは、 証明付きの定理として述べられているが、証明のような手続きを経ずに、そ れらが自明な事実となるような定義があるとうれしいのだ。見晴らしが良い定 式化がほしいのだ。
次に、M. W. Hopkinsの指摘を取り上げよう。彼は、次の対応があると言う(*注3)。
M. W. Hopkinsは、他にもいろいろな対応関係を列挙している。
このような対応関係/類似性があるなら、場の量子論(の一部)と形式言語 理論(の一部)が、なにか共通の構造を持っているはずである。だが、通常の 定式化からは、物理の匂いがしない。物理(場の量子論)との接点が見える形 で形式言語理論を定式化はできないだろうか。
M.W. Hopkinsの指摘は、タワゴトや偶然として片付けるには、あまりにも面 白い話である。もう少しハッキリと事情を理解したいと思った。だが僕は、 「物理⇔計算科学」対応関係の物理側に出てくる、ハミルトニアン、場の量子 論、S行列、ダイソンの公式などの基本概念を知らない。物理の教科書を眺め てみてもサッパリ理解できないで困っていた(*注4)。
眺めてるだけで理解できるほど甘くはないってことだけど、基本的な素養に 欠けているから、トッカカリさえつかめないのだ。過去の不勉強が悔やまれる。
ある日、深谷賢治[1]『ゲージ理論とトポロジー』(*注5)という本をめくっ ていたら、マイケル・アティヤ (Michael Atiyah)による位相的場の量子論 (topological quantum field theory)の公理というのが載っていた。これは、 物理の知識がない僕でも、なんとか意図を理解できた。アティヤの公理が述べ ていることは、位相的場の量子論というのは、有向コンパクト閉多様体を対象 として、同境(コボルディズム)を射とする圏で定義されている関手というこ とらしい。
人名の直後にある[番号]は、後に出てくる参考文献リストの番号を示し ている。
この関手の定義域となる圏には、直和でモノイド積(monoidal product)が 入り、モノイド圏(monoidal category)にもなっている。有向コンパクト閉 多様体の次元を定数nに制限(ただし、空多様体は含める)すれば、n次元の理 論が考えられる。特に次元を0まで落とすと、有限個の符号付き点(signed points, charged points)を対象として、2つの点集合を結ぶ1次元のヒモ集合 を射とする圏が定義域となる。だが、これはつまらない(有限置換群が現れる だけ)。同境を(2+1)次元ユークリッド空間の箱に閉じこめると組みひもの圏 (category of braids)になる。多様体をCW複体に一般化すると、同境はヒモ ではなくて、グラフで与えられる。
グラフによる同境といえば、CorradiniとGadducci[2]のGSモノイダル圏がそ れに近い。だが、向き(orientation)や符号(sign, charge, polarity)を 考えるなら、いっそのことコンパクト閉圏(compact closed category)で考 えた方がいいだろう。そういえば、Kelly & Laplaza[3]のコンパクト閉圏 の構成(*注6)では、signed set(0次元の有向コンパクト多様体)やinvolution(ヒ モ同境に対応)という概念が出てきている。 さらに思い起こせば、P. Katis, N. Sabadini, R.F.C. Walters[5]の論文でも、 同境概念に触れられている(*注7)から、オートマトンのようなシステム達を 同境で関係づけるというアイディアはさほど奇抜ではないかもしれない。
Kelly & Laplazaのオリジナル論文は入手できないので読んでない。JAISTの (今は慶應大学らしい)白旗優 (Masaru Shirahata)[4]さんが書いた論文"A sequent calculus for compact closed categories" 1996 に詳しく解説されている。
"Bicategories of processes" 1995の "6.2 Interpretation of Elgot automata"に同境の絵がある。そして次のように 書いている。
The following `cobordism' picture illustrates the features of an Elgot automaton. The diagram indicates there is a vector-field on state-space of the system governning the motion of the automaton.
僕のオルタナティブな形式言語理論のエッセンスは、このパラグラフに集約 されている。
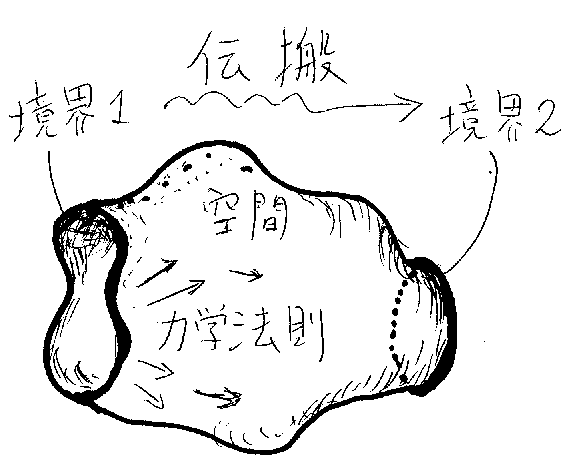
という事情で(ってどんな事情だか?)、形式言語理論を「グラフによる同 境を射とするコンパクト閉圏を使って定式化する」ことを基本ポリシーとする。 この発想は、もともとが物理的なもので、次のように考える。まず、現象の場 である空間がある。その上に力学法則が与えられている。「空間+法則」を力 学系(dynamical systemまたはdynamics)と呼ぼう。力学系の舞台となる空間 は2つの境界を持つ(そう仮定する)。片一方の境界に値を与えると、力学法 則に従って、もう一方の境界まで値が伝搬する。この伝搬(あるいは輸送)現 象によって、「境界1上の値→境界2上の値」という写像が定義される。別な言 い方をすると、力学系に対して“初期値/境界値問題”を解くことにより、2つの境界 をつなぐような関係が得られる。
/* system-with-boundary */

さて、“初期値/境界値問題”を有限離散的な場合に解くには、網羅的な繰り返し計 算をすればいい。この繰り返し計算の部分がハミルトニアンからS行列を作る 操作になっているのだろう(たぶん)。このての繰り返し計算が色々な状況で 出てくることは、随分以前にVaughan Pratt[6]が圏論の言葉使いで指摘してい る。経路積分という手法も同じようなものだろうと思うのだが、僕はよくわかっ ていない。
コンパクト閉圏の「閉」は、は、デカルト閉(cartesian closed)のように、 積に対する随伴としての指数(べき)が存在することを意味する。そして、コ ンパクト閉圏の「コンパクト」は、線形論理におけるテンソルとパー が一致することらしい(確信はないが)。
つまり、多様体の「コンパクト閉」(境界がなく、無闇に拡がっていない) と言葉は同じでも何の関係もないようだ。だが、なんの因果か、(有向)コン パクト閉多様体の同境圏は、実際にコンパクト閉圏にできるし、これは典型的 なコンパクト閉圏だといってもいいだろう。
念のため、出現した順で参考文献を挙げておく。論文は、 CiteSeer.IST (http://citeseer.ist.psu.edu/)や arXiv.org (http://arxiv.org/)で探せば見付かるだろう。
アブラムスキーは、ごく最近(2004年12月)のプレゼンテーションで、強コ ンパクト閉圏(strongly compact closed category)という概念を提案してい る。形式言語理論では、これ(強コンパクト閉圏)のほうが使いやすいような 気がする。
アブラムスキーのプレゼン資料は次のWebページから入手できる。
アブラムスキーを中心とするグループの量子計算/量子プログラミングに関 する論文を1つだけ挙げておく。