ストリング図による複合モナドの計算 (1)

• 関連記事： 図式順テキスト記法

1. はじめに

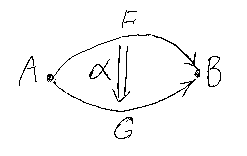
複合モナド^(*注1)を構成する際に、ストリング図を使うと、計算が劇的に 簡単になることがわかった。この記事では、ストリング図を使って、複合モナ ドを実際に構成してみる^(*注2)。これはまた、複合モナド構成を例題とした ストリング図の解説でもある。

この記事のネタ元は次の２つの論文である。

• [1] P.Eklund, M.A. Galan, J.Medina, M. Ojeda-Aciego, A. Valverde "Powersets of Terms and Composite Monads" ( http://www.cs.umu.se/research/reports/2004/007/part1.pdf)
• [2] F. Marmolejo, R.D. Rosebrugh, R.J. Wood "A Basic Distributive Law" ( http://citeseer.ist.psu.edu/315879.html)

この記事でスタック図と呼んでいる図式法は、[1]で使われているもの （Santiago大学のJ. Caruncho Castro、J. Freire Nistalらによる）を指して いる。スタック図は、それ自体としても有用であるが、ペースティング図から ストリング図への翻訳の中間形式として使う。[1]では、スタック図で計算も 行っているが、本記事の計算はもっぱらストリング図に頼る。レイアウトの 自由度や直観的な把握の容易さでは、ストリング図に一日の長があるように思 われる。

2. 「(1)」について

「はじめに」で述べた方針で書き始めたら、ストリング図の描き方まで書い た段階でけっこうな量になったので、いったん切ることにする。この記事で説 明したストリング図（の等式、書き換え規則）を使うと非常に計算が楽になる。 その計算例については続く記事で述べる。

3. ペースティング図からスタック図へ

記号的表現としては、図式順テキスト記法を使う。 α::F⇒G:A→B は、αが関手Fから関手Gへの自然変換であり、FとGは圏Aから圏Bへの 関手であることを示す。

α::F⇒G:A→Bを次のような図で示すことがある。このような図を‘ペースティング図’と呼ぶ。

FIG: ペースティング図

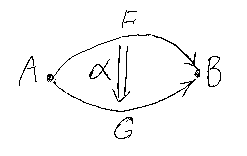
上のペースティング図とまったく同じ内容を、次のような図でも表現できる。こちらは‘スタック図’と呼ぶ。

FIG: スタック図

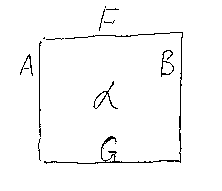
四角形の左右の辺が圏を、上下の辺が関手を表す。四角形内部に自然変換 （の名前）を記入する（F⇒Fの恒等自然変換の場合は四角形内は空白とする）。 関手は左から右、自然変換は上から下と方向を決めているので、いち いち矢印は書かなくてもよい。（人により、右から左、下から上の方向も使う ので注意！）

次は、複合的なペースティング図と、それに対応するスタック図の例である。

1. α:: F;;G ⇒ H : A→C
2. β:: F;;F ⇒ K;;L : A→A

FIG: ペースティング図とスタック図

4. ストリング図

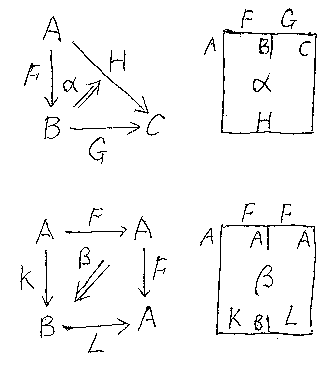
平面内で、一筆書きできる“交差しない境界線”で囲まれた領域を‘部屋’ （chamber）と呼ぶ。平面内に描かれた有向グラフDが、部屋Rに対する‘スト リング図’だとは、次を満たすことである。なお、‘開いた辺’とは、始点ま たは終点のどちらか一方のノードを持たない辺であり、ここではグラフに開い た辺を認める。

1. すべてのノードは部屋の内部にある。
2. 開いた辺は、必ず部屋の境界と交差する。

ストリング図の‘面’とは、グラフの辺と部屋の境界によって囲まれた領域 であり、その内部に辺もノードも含まないものである。

この記事では、関手と自然変換の計算のためにストリング図を使うので、さらに 次を仮定する。

• すべての面は圏の名前でラベル付けされている。面のラベルは一意的であ る必要はない。
• すべての辺は関手の名前でラベル付けされている。辺のラベルは一意的で ある必要はない。
• すべてのノードは自然変換の名前でラベル付けされている。ノードのラベ ルは一意的である必要はない。

5. スタック図からストリング図へ

まずは事例を見るのが早いだろう。以下は、α:: F;;G ⇒ H : A→C と β:: F;;F ⇒ K;;L : A→A のスタック図からストリング図への描き換えである。点 線は部屋の境界である。

FIG: スタック図からストリング図へ

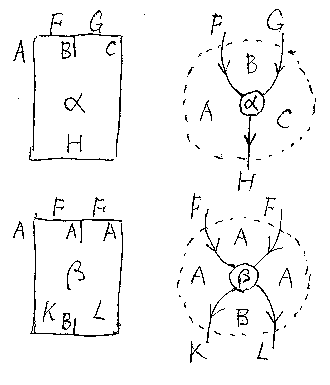
描き替えの手順は次のとおり：

1. スタックの箱を部屋とする。ただし、適宜、形状を変形してもよい。
2. スタックの箱内部にある自然変換に対してノードを描き、自然変換の名前 でラベル付けする。
3. 関手を、部屋の外部と自然変換ノードを結ぶ有向辺として描き、ラベル付 けする。
4. 面を圏の名前でラベル付けする。

さらに、簡略化のために次の規約を適用してもよい。

1. 部屋の境界は明示的に描かない。
2. 有向辺の方向は常に上から下として、矢印は描かない。
3. 面のラベルを適宜省略する。特に、すべての面に同じラベルが付くとき（モナドの計算はその例）は 省略しても何の問題もない。

6. モナドの定義

以下、圏Cを１つ選んで固定する。F, Gなどは圏CからCへの自己関手 （endofunctor）である。圏Cの恒等関手は常にIと記す。関手Fと自然変換μ:: F;;F⇒F、自然変換η:: I⇒F の組(F, μ, η)が‘モナド’だとは、次の結合 律と単位律を満たすことである。

 (F;;F);;F =[μ;;F]⇒ F;;F =[μ]⇒ F
 =================================== 結合律
 F;;(F;;F) =[F;;μ]⇒ F;;F =[μ]⇒ F

 I;;F =[η;;F]⇒ F;;F =[μ]⇒ F
 ============================== 単位律1
 I;;F ⇒ F

 F;;I =[F;;η]⇒ F;;F =[μ]⇒ F
 ============================== 単位律2
 F;;F ⇒ F

結合律をより正確に述べるには、(F;;F);;F と F;;(F;;F)のあいだを結ぶ自 然変換（associativity）α:: (F;;F);;F ⇒ F;;(F;;F) を導入すべきだが、 今回はこれを省略して、(F;;F);;F = F;;(F;;F) = F;;F;;F として扱う。

7. モナドのストリング図による表現

モナドの結合律と単位律は、自然変換の可換図式で表現できる。その可換図 式から、いくつかの等式が得られる。等式の左辺／右辺はそれぞれ自然変換で ある。左辺／右辺をストリング図で表現すると、結合律／単位律はストリング 図の等式として表現できる。

結合律を例に、ストリング図の等式を構成してみる。まずは可換図式であるが、 簡略化のために「;;」を省略し、矢印は「⇒」ではなくて「→」を使う。

FIG: 結合律を表す可換図式

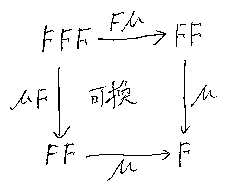
スタック図を中間において、可換図式からストリング図を導いてみる。

FIG: 結合律を表すスタック図、ストリング図の等式

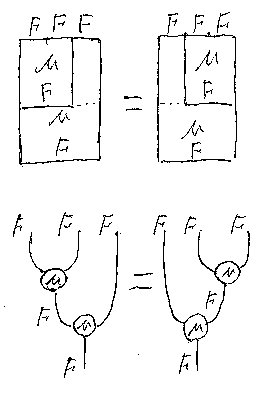
同様な方法で、2つの単位律をストリング図の等式で描くと次のようになる。 名前を記入してないノードは、自明な自然変換（自然同値） I;;F ⇒ F、F;;I ⇒ F である。

FIG: 単位律を表すストリング図の等式

8. 自然変換のアイコン

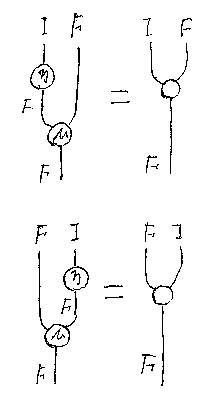
頻繁に登場する自然変換は、名前ラベルではなくてアイコンで描くことにする。

1. モナド乗法は、ラベルなしの白丸で表す。
2. モナド単位は、三角で表す。
3. 恒等自然変換はノードを描かない。
4. I;;F ⇒ F、F;;I → F は合流として描く。
5. F ⇒ I;;F、F → F;;I は枝分かれとして描く。

アイコンを使って、結合律と2つの単位律を表すと次のようになる。

FIG: アイコンを使ったストリング図の等式