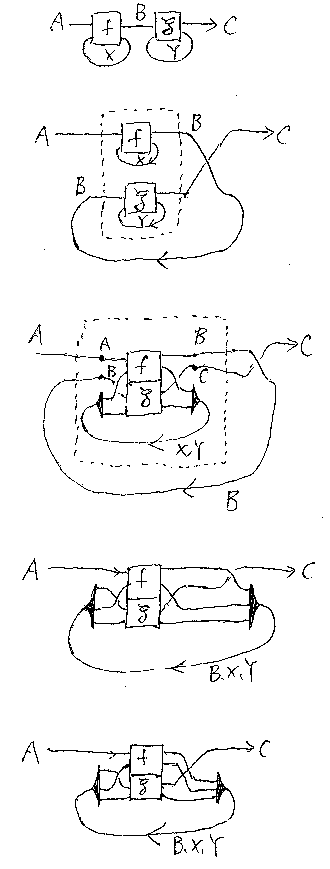
トレースとモノイド積／結合

檜山正幸 (HIYAMA Masayuki)
Tue Jul 04 2006:start

トレース付きモノイド圏（traced monoidal category）における、“トレース とモノイド積”、“トレースと結合”の関係を示す。

目次

1. はじめに

以前、記事「スーパーポージング公理からスーパーポー ジング定理へ」において、縄跳びの補題を使ってオリジナル形スーパーポー ジング公理を（単純化されたスーパーポージング公理から）示した。よく似た 議論で、2つのトレースされた射のモノイド積を1つのトレースにまとめる公式 が得られる。まずこれを示す。

次に、記事「トレース付きモノイド圏における結合」で示した公式と、トレースと積の関係を組み合わせて、 2つのトレースされた射の結合を1つのトレースにまとめる公式をを示す。

2. トレースとモノイド積

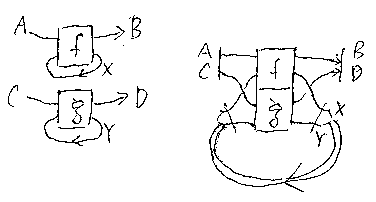
(C, +, 0, σ, Tr)はトレース付きモノイド圏（traced monoidal category）だとする。Cの射 f:A+X→B+X, g:C+Y→D+Yに対して：

・ トレースとモノイド積の関係

TrXA,B(f)+TrYC,D(g) ≒ TrX+YA+C,B+D[(A+σC,X+Y);(f+g);(B+σX,D+Y)]

FIG: トレースとモノイド積の関係

次の縄跳びの補題を使う。

・ 縄跳びの補題（一般形）

(A+σC,X);(f+g);(B+σY,D)=(σA,C+X);(g+f);(σD,B+Y)

説明は図の後：

FIG: “トレースとモノイド積の関係”の証明

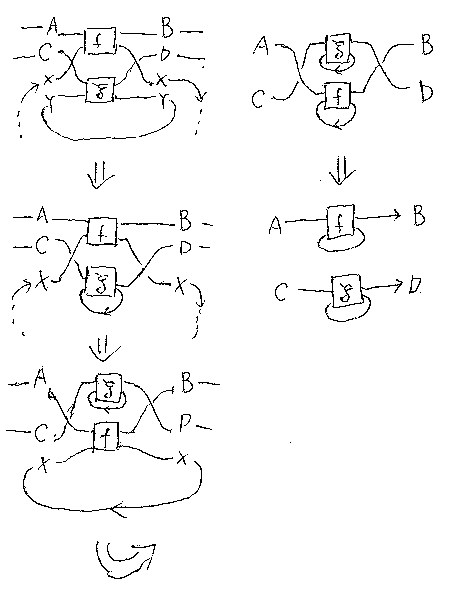
TrX+YA+C,B+D[(A+σC,X+Y);(f+g);(B+σX,D+Y)] から TrXA,B(f)+TrYC,D(g) に向かって変形していく。

  1. TrX+Y[...]を、バニッシングを使って TrX(TrY[...]) にする。
  2. TrY[...]のループを、タイトニングを使って縮める。
  3. 縄跳びの補題で、TrY(g) を上に持って行く。
  4. TrX[...]のループを、タイトニングを使って縮める。
  5. 左右にあるクロスをまとめて消滅させると、求める結果が得られる。

3. トレースと結合

f:A+X→B+X、g:B+Y→C+Y とする。

・ トレースと結合の関係

(TrXA,B(f));(TrYB,C(g)) ≒ TrB+X+YA,C[(A+σB,X+Y);(f+g);(σB+X,C+Y)]

FIG: “トレースと結合の関係”の証明
  1. 記事「トレース付きモノイド圏における結合」 で示した f;g ≒ TrBA,C[(f+g);σ] を使って、結合をモノイド積 とトレースで書く。
  2. トレースされた射のモノイド積を、先に示した公式で1つのトレースにまとめる。
  3. 内側のループをタイトニングで広げて、さらにバニッシングで1つのトレー スにする。
  4. 2つのクロスを1つのクロスにまとめて、求める結果が得られる。