コンパクト閉圏

• 関連記事：お絵描き圏論
• 関連記事：コンパクト閉圏を定義する

• 関連記事：「圏論」インデックス

1. はじめに

2005年2月8日の時点において、Googleで "compact closed categories"（あ るいは、"compact closed category"、「コンパクト閉圏」）で日本語のペー ジを探しても、なんと2件しか出てこない。1件はこのChimairaサイトで、もう 1件は、 SLACS（スラックス; Symbolic Logic And Computer Science）1996年の発表プログラム内の、白 旗優（慶応大学商学部）氏発表のタイトル「A sequent calculus for compact closed categories」である。ということは、コンパクト閉圏に興味を持つ人 なんて事実上いないってことだ。かなりトホホな気分、寂（サビ）しいなぁ。

Web全体では、"compact closed categories"で225件がヒットするから、それ なり（かぁ？）の人が興味を持っている。が、日常的なプログラミング （everyday programming）に対して、コンパクト閉圏で考えよう、なんて言う 奴はたぶん僕だけかもしれない。哀（カナ）しいなぁ。

そういうわけだから、この記事の読者はたぶん僕ひとりだろう。が、自 分自身の備忘のために書いておきたい。…… しかし、侘（ワ）びしいなぁ。

備忘目的だから、脈絡もなく雑多なことを書く。もちろん、全然セルフコン テインドではない。が、コンパクト閉圏をソフトウェアの理論と実践に応用す る人が出現することを少しは期待して、そのような人には多少面白そうな話に はしたい。

（この段落は、記事を書き終えた後に書いている：）面白いと（少なくとも 僕には）思えることがいくつかあるのだけど、定義の周辺をウロウロしている うちに疲れたので、とりあえずは適当なところで区切って、続きは別な記事に 書くことにする。

[2005-07-05追記]第4節の「なんで左？」に書いておいた疑問は、僕の深読み し過ぎであったことが判明。左随伴の「随伴」は随伴対とは何の関係もなくて、 「双対」とほぼ同義語だった。このへんの事情は、別な記事として書くかもし れない。

2. 参考文献

最初にネタもと（情報源）を挙げておく。ただし、星印が付いたものは入手 できないので、まったく見てない。他は、 インターネット（CiteSeer.IST （http://citeseer.ist.psu.edu/）、 arXiv.org （http://arxiv.org/））で探せば見付かる。

1. [Abr93]* S. Abramsky "Interaction Categories" 1993 (unpublished lecture notes)
2. [Abr04] QDay Paris Dec. 2004 のスライド
3. [AC04] Samson Abramsky, Bob Coecke "A categorical semantics of quantum protocols" 2004
4. [AGN95] Samson Abramsky, Simon Gay, Rajagopal Nagarajan "Interaction Categories and the Foundations of Typed Concurrent Programming" 1995
5. [AD04] Samson Abramsky , Ross Duncan "A categorical quantum logic" 2004
6. [JSV96]* Andre' Joyal, Ross Street, Dominic Verity "Traced monoidal categories" 1996
7. [Has97] Masahito Hasegawa "Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi" 1997
8. [KL80]* G.M. Kelly, M.L. Laplaza "Coherence for compact closed categories" Jurnal of Pure and Applied Algebra, 19, 1980
9. [Shi96] Masaru Shirahata "A sequent calculus for compact closed categories" 1996

[JSV96]と[KL80]はそれぞれ、トレース付きモノイド圏とコンパクト閉圏の原 典らしいが、入手できない。トレース付きモノイド圏とコンパクト閉圏の定義 は、[Has97]と[Shi96]で言及されているので、僕はそれで知った。

[Abr93]は、コンパクト閉圏を計算科学／プログラミングに応用したものらし いが、unpublishedだから入手できない。ただし、[AGN95]でその内容を知るこ とができるようだ。とはいっても、[AGN95]は60ページ以上あるし、ウチのプ リンタが調子悪いときに印刷したので、あっちこっちかすれていて（って、そ れが理由か？）まったく読んでない^(*注1)。

僕が最近よく眺めているのは、プレゼン用のスライド[Abr04]（ http://web.comlab.ox.ac.uk/oucl/work/samson.abramsky/talks.htmlの `QDay Paris December 14 2004: Talk on `Abstract Scalars and Free Constructions'）だ。イラストがたくさんあり、概要が箇条書きで書いてある。 僕は、詳しい説明を読んでもどうせ分からないからこれで十分だ:-)。

3. とりあえず定義

まず、コンパクト閉圏の定義から。僕のネタもとは[Shi96]の第2節だが、お そらくは[KL80]で最初に定義されたのだろう。事前に、モノイド圏（monoidal category）Cの対象Aに対して、その左随伴（left adjoint）という概念が必要 だ。左随伴は、必ずしも対称でないモノイド圏でも定義できる（が、非対称ケー スで意味があるのだろうか？ 僕はよく分からない）。以下、×はモノイド積 （monoidal product, multiplication）、Iはモノイド単位（monoidal unit） だとする。f:A→B を、A -(f)→Bのようにも書く（矢印の上にfを書けないの で代替表現）。また、対象Xの恒等射（identity）を同じ記号Xで表す^(*注2)。 「≒」はisomorphicのつもりである。

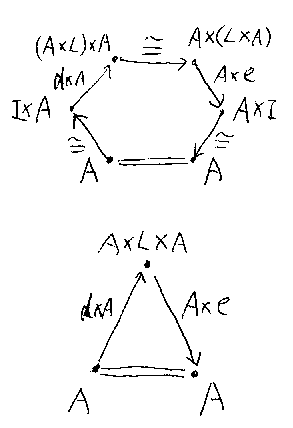
対象Lと、d:I→A×L、e:L×A→I の3つ組(L, d, e)がAの‘左随伴’であると は、次の等式が成立することである。

1. [A≒I×A -(d×A)→(A×L)×A≒A×(L×A) -(A×e)→A×I≒A]の結合 = A
2. [L≒L×I -(L×d)→L×(A×L)≒(L×A)×L -(e×L)→I×L≒L]の結合 = L

ここで、≒は標準的に定まる同型射と解釈する。これらの等式を可換図式で 描くと、六角形になるが、なぜか‘三角恒等式’（triangular identities） と呼ばれている（[Abr04]）。おそらく、自明な≒を同一視すると三角形の可 換図式になるからだろう（下の図）。

FIG: 六角形と三角形

/* triangular */

三角形に簡略化された形で等式を書き直せば、次のようになる。

1. [A -(d×A)→A×L×A -(A×e)→A]の結合 = A
2. [L -(L×d)→L×A×L -(e×L)→L]の結合 = L

Aに対してその左随伴Lが一意的に確定するわけではない（存在しても、同型 だけの違いはあり得る）。A|→A^*、A|→η_A、A|→ε_A という一意的な 割り当てがあって、その(A^*, η_A, ε_A) がAの左随伴を与えていて、も とのモノイド圏Cが対称のとき、これらをまとめた構造(C, (-)^*, η, ε)を ‘コンパクト閉圏’と呼ぶ。

以上は、[Shi98]に基づいて述べたが、Abramskyは、η_A、ε_Aの型（プロ ファイル）を、I→A×A^*、A^*×A→Iではなく、I→A^*×A、A×A^*→Iと している。別にどっちでもいいのだが、混乱のもとになるかもしれない。例え ば、三角恒等式を2種の定義に沿って書いてみると、次のようになる。

• [A -(η_A×A)→A×A^*×A -(A×ε_A)→A]の結合 = A
• [A -(A×η_A)→A×A^*×A -(ε_A×A)→A]の結合 = A

いま「別にどっちでもいい」と言ったが、ほんとにどっちでもいいことを示 すのは全然自明ではない。「結んでない輪は、ほどけてまっすぐになる」こと を意味するヤンキング公式が必要だ。そのヤンキング公式を示すためには、コ ンパクト閉圏のめぼしい性質を前もって調べておく必要がある。

めぼしい性質には次のようなものがある。

1. （A×B)^* ≒ A^*×B^*
2. I^* ≒ I
3. A^** ≒ A
4. η_A* ≒ η_A;σ_A*,A
5. ε_A* ≒ σ_A*,A;ε_A

Kelly & Laplazaの定義では、これらはすべて自明とは言えない定理になる。 が、コンパクト閉圏を使う側としては、基本的な性質は最初から列挙されてい たほうがいい。Kelly & Laplazaの定義は、公理の最小化を重視しているよう だが、冗長でも、もっと計算に便利な定式化があったほうがいいと僕は思う。

4. なんで「左」？

まず、Aに対する(A^*, η_A, ε_A)を、なぜ左随伴と呼ぶのだろう。左随 伴といえば、関手の随伴対が思い浮かぶ。背後に随伴対があるのだろうか？ あるといえばある。が、“左”随伴じゃないと思うのだけど…、以下に説明す る。

Cの対象Xに（右から）Aをかける（モノイダル積する）関手を‘Aテンソリン グ’と呼ぶことにする。つまり、T_A(X)=X×AとしたときのT_AがAテンソリ ングだ。Aテンソリングの右随伴関手があれば、それをE_Aと書いて‘Aベキ’ と呼ぶことにする。E_A(X)は、X^Aとか[A, X]とかA-・X（実際は黒丸でなく て白丸）とか書かれる。呼び方もいろいろで、指数（exponent）、 内部hom（internal hom）、余テンソル（cotensor）などと呼ぶ（用語の微妙 な差は下のノートを見よ）。論理で言えば含意（implication）だし、集合圏 では関数集合／関数空間である。[Shi96]では、[A, X]をclosure operationと 呼んでいる。すべての対象Aに対してclosure operation [A, -]を持っている 圏が(monoidal) closed categoryだから、まー、ツジツマがあっているような 気もする。が、閉演算（closure operation/operator）は、順序構造や位相で 全然別な意味で使われることもある（例：クラトフスキーの閉演算）。

AテンソリングT_AとAベキE_Aは随伴だから、次の自然な同型が存在する。

• C(T_A(X), Y)≒C(X, E_A(Y))

• C(X×A, Y)≒C(X, [A, Y])

ところで、コンパクト閉圏では、[A, Y]がY×A^* で与えられる、つまり、 次が成立する；天下りだが、以下ではこの事実を仮定して話をする^(*注3)。

• C(X×A, Y)≒C(X, Y×A^*)

よって、AベキはA^*テンソリングに他ならない。A^*テンソリングをT^Aと 書けば（添字が二重になるのがイヤなので、Aを上付と下付で区別した）、次 のような随伴関係（adjunction）がある。

• C(T_A(X), Y)≒C(X, T^A(Y))

これは、次の主張と同じ事だ。

1. T_Aは、T^Aの左随伴である。
2. T^Aは、T_Aの右随伴である。

1. `×A'は、`×A^*'の左随伴である。
2. `×A<sup>*</sup>'は、`×A'の右随伴である。

5. 単位と余単位

以下では、Abramskyに従って、η_A:I→A^*×A、ε_A：A×A^*→I とい う定義を採用しよう。記号ηとεを使うのもAbramskyのとおりである （[Shi98]では、dとeを使っている）。ηを‘単位’（unit）、εを‘余単位’ （counit）と呼ぶ。A^*は、Aの‘双対’（dual）と呼ぶようだ。「双対」と いう言葉も使われすぎだけど、この場合はふさわしいと思えるので、遠慮しな いで「双対」を使うことにする^(*注4)。よって、A|→A^* は‘双対化演算’ （dualizing operator）と呼ぶことにする。双対化 A|→A^* は、定義の上か らは関手にはなっていないし、η、εもとりあえずは自然変換とは言えない。

Abramsky流の定義では、 Aベキ関手[A, X]はA^*×Xと、左から双対を掛け算する形になっている。それ で、T^A(X) = A^*×X と変更しておく。いずれにしても、T_AとT^Aが随伴 対になることは変わりない。

随伴対に対して、単位と余単位という概念がある。習慣的記号法として、単 位にη、余単位にεをあてるが、それではコンパクト閉圏の単位／余単位と区別 が付かなくなるので、ΠとΘを随伴対の単位／余単位を表すために使う。

以下で何をしたいかというと、コンパクト閉圏の単位／余単位と随伴の単位／ 余単位がどう関係しているかを見たいのである。とりあえず、T_AとT^Aが随 伴対であるという事実から出発する。随伴対から単位／余単位を構成する方法 を教科書（Mac Lane、Borceux）どおりにたどってみる。

単位とは、Xごとに決まる射Π_X:X→T^A(T_A(X)) なのだが、実際には、 随伴対に基づいて構成されるから、Π<T_A, ψ, T^A>_X のように書くべき だろう。ここで、<T_A, ψ, T^A>が随伴対の構造全体を表している、ψは C(T_A(X), Y)≒C(X, T^A(Y))の同型を与える写像 （方向はC(T_A(X), Y)→C(X, T^A(Y))）だとする。

C(T_A(X), Y)≒C(X, T^A(Y))において、Y=T_A(X)と置けば、 C(T_A(X), T_A(X))≒C(X, T^A(T_A(X)))となる。左辺の集合内に は、T_A(X)の恒等射が存在するから、それのψによる像をgとすると、 g∈C(X, T^A(T_A(X)))、つまり、g:X→T^A(T_A(X))。このgは、随伴対を もとにして、対象Xごとに指定されるので、g=Π<T_A, ψ, T^A>_Xと書く。 が、事情がはっきりしていれば、Π_Xと略記してよい。T_AとT^Aの随伴 構造がAで決定されるから、Π^A_Xという書き方も使うことにする。 X=T^A(Y)と置いて、同様な議論をすれば、 余単位Θ<T_A, ψ, T^A>_Y:T_A(T^A(Y))→Yが得られる。

T_AとT^Aを開いて書けば、次のようになる。

• Π<T_A, ψ, T^A>_X:X→A^*×(X×A)
• Θ<T_A, ψ, T^A>_Y:(A^*×Y)×A→Y

特に、XとYをモノイド単位Iとすれば、次の形になる。

• Π<T_A, ψ, T^A>_I:I→A^*×(I×A)
• Θ<T_A, ψ, T^A>_I:(A^*×I)×A→I

A^*×(I×A)≒A^*×A、(A^*×I)×A≒A^*×Aを使えば、形の上では、 Π<T_A, ψ, T^A>_I=Π^A_Iはη_Aと、 Θ<T_A, ψ, T^A>_I=Θ^A_Iはε_Aと似ている（Θのプロファイルはε とちょっと違っているが）。これらは、ほんとにコンパクト閉圏のηとεなの だろうか。

6. ネームと余ネーム

前節の問題を考える上で、Abramskyが導入したネーム（name）と余ネーム （coname）を使うと便利である。コンパクト閉圏Cの射f:A→Bに対して、fをデー タまたは点とみなしたものを定義できる。それをfのネームと呼ぶ。ノイマン 式コンピュータでは、機能・動作を実現するプログラムも、格納されたデータ とみなせる。fのネームとは、「データ／点とみなしたf」ということになる。 Abramskyは、fのネームをゲーデル・コーディングの記号で表しているが、機 能・動作・手続き・アルゴリズムなどをデータ／値とみなすことは、確かに一 種のゲーデル・コーディングだ。

ネームを定義するには、C(A, B)≒C(I, A^*×B)という同型を使う。これは、 C(A, B)≒C(I×A, B)とC(I×A, B)≒C(I, [A, B])をつなげればよい（[A, B]=A^*×Bに注意）。C(A, B)≒C(I, A^*×B)を与える同型写像をΦ_A,B とすると、 [f]=Φ_A,B(f)として、この[f]を、fの‘ネーム’と呼ぶ。

余ネームは、C(A×B^*, I)≒C(A, B^**×I)とC(A, B^**×I)≒C(A, B)から定義される同型Ψ_A,B: C(A×B^*, I)→C(A, B)を使って定義され る。つまり、fの‘余ネーム’]f[は、]f[=(Ψ_A,B)^-1(f)である。ただ し、B^**≒Bは別に示す必要がある。

AとBが同じときは、Φ_A,A:C(A, A)→C(I, A^*×A)となる。C(A, A)には Aの恒等射Aがあるから、そのネーム[A]はI→A^*×Aである。同様に、 Ψ_A,A:C(A×A^*, I)→C(A, A)だから、]A[:A×A^*→ Iとなる。

[AC04]によれば、次が成立する（簡単に示せる、下のノート参照）。

• [A]=η_A
• ]A[=ε_A

7. 随伴対の単位／余単位とコンパクト閉圏の単位／余単位

η_A=[A]だから、[A]=Π<T_A, ψ, T^A>_Iが示せれば、η_A=Π<T_A, ψ, T^A>_Iだといえる。実際には、この等式そのものを文字通りに示すこと はできないのだが、“[A]を定義するための自然変換”と、 “Π<T_A, ψ, T^A>_Iを定義するための自然変換（の若干の変形）”が事 実上等しいことが示せる。さてまずは、[A]とΠ<T_A, ψ, T^A>_Iの関係を 見るために、ネームと随伴単位の定義を、もっとあからさまに書き下してみよ う。

ネーム[A]を定義するために使ったΦ_A,Aは、2つの同型C(A, A)≒C(I×A, A)とC(I×A, A)≒C(I, [A, A])をつないだものであった。 もっと具体的にΦ_A,Aを書いてみる。まず、C(A, A)≒C(I×A, A)の同型を 与える写像をλ_Aとする。C(I×A, A)≒C(I, [A, A])同型を与える写像のほ うは、随伴<T_A, ψ, T^A>に現れたψを使って、ψ_I,Aと書ける。だか ら、Φ_A,A=λ_A;ψ_I,A。

これを使えば、恒等射Aのネーム[A]の定義は次のようになる。

• [A]=(λ_A;ψ_I,A)(A):I→A^*×A

一方、Π^A_Iは、C(T_A(I), T_A(I))≒C(I, T^A(T_A(I)))を使って定義さ れる。この同型写像は、ψを使って、ψ_I,I×Aと書ける。Π^A_Iとは、 T_A(I)つまりはI×Aの恒等射を、ψ_I,I×Aに代入したものだから、 次のように書ける。

• Π^A_I=ψ_I,I×A(I×A):I→A^*×(I×A)

ここから先は図式でみたほうが早いだろう（下）。

FIG: [A]とΠ^A_Iの関係

/* unit-name */

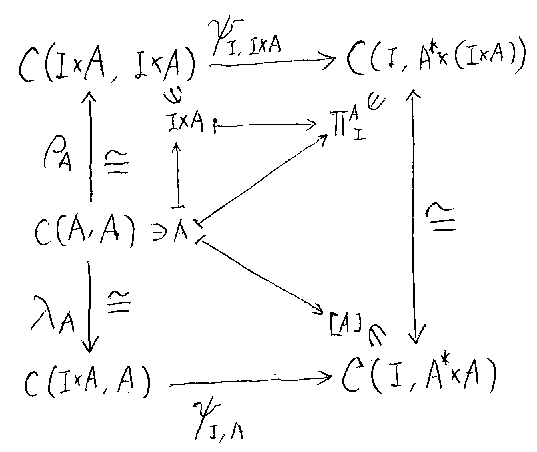
対象Aの恒等射はC(A, A)のなかにあるが、C(A, A)から出る 写像λ_A;ψ_I,Aは、別な経路を通った C(A, A)≒C(I×A, I×A) -(ψ_I,I×A)→C(I, A^*×(I×A))≒C(I, A^*×A) と同じである。そのとき、Aの恒等射とI×Aの恒等射が移りあっている。

上に出てくる同型写像C(A, A)→C(I×A, I×A)をρ_Aとすれば、 ρ_A;ψ_I,I×Aとλ_A;ψ_I,Aは、C(I, A^*×(I×A))≒C(I, A^*×A) の同型を後結合（post-compose）することで互いに移りあう。そのとき、[A]とΠ^A_Iも、互 いに移りあうのである。だから、[A]とΠ^A_Iは同一視できるといってもい いだろう。

結局、T_A、T^Aという随伴対から作った単位（と呼ばれる自然変換）Π^A のIにおける値（I→T^A(T_A(I))というCの射）は、Aのネーム[A]と同一視でき、 したがって、η_Aとも同一視できる、ということになる。おおざっぱにいえば、 次が成立する。

• Π^A_I = η_A

これをもって、随伴対の単位とコンパクト閉圏の単位は、（ほぼ）同じもの だといってもいいだろう。控えめにいっても、Π^A_Iとη_Aはハッキリ とした関係で結ばれている。Θ^A_Iとε_Aに関しても同様である。

8. まとめ

脈絡もなく雑多なことを書いたので、ここでまとめておく。

• コンパクト閉圏において、“Aによる掛け算T_A”と“A^*による 掛け算T^A”は互いに随伴である。
• このとき、A^*による掛け算は右随伴である。
• 随伴対<T_A, ψ, T^A>により定義される随伴単位をΠ^Aとする。 Π^Aは、パラメータAを持つ自然変換の族であり、 Π^A_X：X→T^A（T_A(X))、つまりΠ^A:Id_C⇒T^A・T_Aとなる （「⇒」は自然変換を表す矢印）。
• Π^A_I:I→T^A（T_A(I))は、η_A:I→A^*×A と事実上等しい。
• よって、コンパクト閉圏の単位η_Aは、随伴対<T_A, ψ, T^A>の随伴単 位（自然変換）の特殊値を取ったと言ってもよい。