/* straight-junction */
「誰でもわかる『コンパクト閉圏』」を目指して書き始めた記事。だが、前 書きが長くなりすぎて、本編に至ってない。結局この記事は、前置きの部分だ け。コンパクト閉圏は(図形的に見れば)、まっすぐな線分だけから交差や曲 がり(回転)も取り入れる形で“進化した圏”、と位置付けられることを示す。
「コンパクト閉圏」という記事を書い たが、これは「脈絡もなく雑多なこと」を備忘目的で記したものだ。そのため、 系統的な説明にはまったくなってない。で、この記事でなにか系統的な話をす るかというと、そうではなくて:-)、もっと脈絡もなく雑多なことになる。
「コンパクト閉圏」の6節の短いノー ト「ネーミング同型のあからさまな表示」で、コンパクト閉圏は、どことなく 算数っぽい雰囲気があると書いた。アブストラクト・ナンセンスと揶揄(*注1) されるほどに、抽象度が高いメタ領域を扱っていると言える圏論のどこが算数 なんだ? という疑問は当然だろうから、そのへんについてインフォーマルに 補足したい。
「アブストラクト・ナンセンス」は必ずしも悪口とは限らない。抽象度を上 げた一般論により、華麗に決着を付ける論法/手法に対する誉め言葉でもある。
実際のところ、コンパクト閉圏における計算とは、「まっすぐな線分」、 「交差する線分」、「半円形」を組み合わせて遊ぶ図形ゲームに過ぎないのだ。
題名や前節「はじめに」から推測はつくと思うが、この記事は、コンパクト 閉圏についての、非常に平易な解説を意図して書き始めた。どのくらい平易かと いうと、完全にセルフコンテインドで、小学生でも理解できるように説明でき るのだ。ジョーダンでもウソでもない。いや、ホント、ホントの話ですよ!
コンパクト閉圏は本質的にやさしいものなのだ。小学3、4年生なら、計算の ルールを理解できるし、実際の計算も遂行できるだろう。その計算とは、「図 形ゲームに過ぎない」のだから。その図形ゲームは、レゴ、プラレール、テト リスを混ぜたような感じのものだ。本物の玩具やゲームに仕立てることもでき るだろう(それが遊びとしてトッテモ面白いという保証はないが)。
この図形ゲームで遊んだ子供達が育てば、コンパクト閉圏とその応用は、ほ んとに算数レベルの話になるだろう。 中学生くらいで、Abramsky の論文が読めたりするかも。
と、そういう「誰でもわかる『コンパクト閉圏』」を書き始めたのだが、ど うも前置きが長くなってしまった。そう、実は前置きの部分だけで切り落とし たのがこの記事です。したがって、この記事自体は「誰でもわかる」になって ません。(とはいえ、それほど多くの予備知識を仮定しているわけではない。)
だから、この先は読まないという選択もあるし、それは賢明な選択かもしれ ない。が、もう一度繰り返しておく:コンパクト閉圏を、小学生でも理解でき るように説明できる。ジョーダンでもウソでもない。次の記事は、ほんとに 「誰でもわかる『コンパクト閉圏』」だ -- と、近く出るであろう 次の記事(*注2)の宣伝はしておく。
「次の記事」とは、時間的にこの記事にすぐ後続するという意味ではない。 同じ話題の続きとなる記事、という意味です。
はい、ここから先は、長くなりすぎた前置きです。
圏論のいいところは、絵を描いて説明や計算ができるところだ。よく使うの は、点が対象、矢印が射を表す図式だ。そのような図式が「可換だ」と主張す ることが、一群の等式を書き下す代わりになる。
対称モノイド圏(symmetric monoidal categories)、トレース付きモノイド 圏(traced monoidal categories)、コンパクト閉圏(compact closed categories)では、特に絵が強力な武器になる。 以前に書いた「ETBダイアグラム」という記事は、対 称モノイド圏に絞って“絵の描き方”を説明したものだ。話を簡単にするため に、自然数{0, 1, 2, ...} とその足し算が、対象(圏のobjects)のモノイド 構造を与える例に限っているが、一般の対称モノイド圏でも同じように絵を描 ける。
記事「ETBダイアグラム」において、僕はジャンクション(接合器、つなぎ) という概念を提案した。対称モノイド圏に出てくるジャンクションはストレー ト・ジャンクションとクロス・ジャンクションの2種類である。もう少し正確 にいうと、ジャンクションは圏の対象でパラメータ付けられた族として登場す る。対象Aに対するストレート・ジャンクションをιA、対象AとBに対するク ロス・ジャンクションをσA,Bと書くことにする(これは記事「ETBダイア グラム」と異なる記号法だ(*注3))。さらにモノイド積は+、モノイド単位 は0で示す。
記事「ETBダイアグラム」では、Bergstra/Stefanescuに従って、ストレート・ ジャンクション(自明なジャンクション)をIA、クロス・ジャンクション をXA,Bと書いた。この記事では、ジャンクションはすべてギリシャ文字で 表すことにした。
ストレート・ジャンクションは、あらゆる圏に存在する恒等射のことである。 クロス・ジャンクションのほうは、対称モノイド圏に特有なものである。圏/ 対称モノイド圏では、ジャンクションは特殊な射に過ぎない。が、常に「ジャ ンクション = 特殊な射」とは言えないのである。そのあたりを次節以降で説 明する。
ジャンクションとは、固有な能力を持たず、その名の通り“対象のあいだを つなぐ”だけに使われる圏論的部品のことである。個々の圏の個性とは無関係 に、ある類に属する圏(*注4)に最初から備え付けられている接合機能が ジャンクションなのだ。
「ある類に属する圏」とは何かといえば、形式的圏論(セオリー)を1つ固定 したときのモデル圏に属する圏である。モデル圏は“圏の圏”になる。いろい ろな形式的圏論を一度に考えれば、たくさんの圏論達がインスティチューショ ン(institution)を作ることになるが、そのとき、モデル圏達が再び作る圏 は、“圏の圏の圏”である。
射を箱で表すなら、ストレート・ジャンクションは直線で表すのがふさわし いだろう。ストレート・ジャンクションの特徴は、任意に挿入したり消したり できることだ。例えば、ιA;ιA;f = ιA;f = f など。よって、ストレー ト・ジャンクションは、必要なだけいくらでも伸ばしたり、あるいは縮めたり できる(長さ0まで縮めてもよい)ワイヤーである(下の図)。
/* straight-junction */

クロス・ジャンクションは、ストレート・ジャンクションよりは多少の存在 感がある。クロス・ジャンクションを無条件に挿入/削除することはできない。 しかし、σA,B;σB,A=ιA+B だから、2つ連続して結合するとそ の効果が消えることがある。これを絵に描くと、2回の交差を引き伸ばしてい ることになる。
/* cross-stretching */
より一般に、交差や曲がりがあるワイヤーをストレートにする操作を‘引き 伸ばし’(ストレッチング)と呼び、引き延ばし法を与える法則は‘引き伸ば し公式’(stretching formula)と呼ぶことにしよう。σA,B;σB,A= ιA+B は引き伸ばし公式の一例である。
ストレート・ジャンクションは、最初から伸びているので、引き伸ばし公式 が自明に成立している。つまり、退化したケースと考えよう。
対称モノイド圏におけるフィードバック・ジャンクションという概念を導入 する。対象Aに対するフィードバック・ジャンクションをθAと書くことにす る(つまり、1つの対象でパラメータ付けられた族である)。θAを絵で描く のは簡単で、次のようになる。
/* feedback-junction */
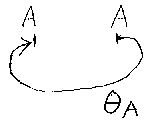
ストレート・ジャンクションはまっすぐな線だったが、フィードバック・ジャ ンクションは、グルリと一回りして戻ってくる。例えば、f:A→Aのような射と フィードバック・ジャンクションθAを組み合わせると、入出力が還流して 消えてしまう(0→0の射になる)。
/* total-feedback */
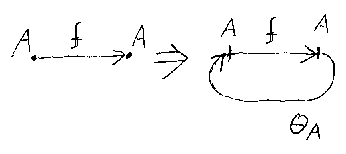
絵で見るといたって簡単なフィードバック・ジャンクションだが、これは、 圏の射としては解釈できない。仕方がないので、f:X+A→Y+Aという形の射にフィー ドバック・ジャンクションθAを取り付ける操作を定式化に使う。 仮に、「fにθAを取り付ける」演算を「θA%f」とでもして、パラメータ X, Y, Aを持ったオペレータTrAX,Yを、TrAX,Y(f)=θA%fとして 定義するのである。このオペレータTrをトレースと呼ぶ。
オペレータTrの性質は7つの公理にまとめられて、そのような公理を満たす圏 としてトレース付きモノイド圏が定義される。が、すべての対象Aに対するフィー ドバック・ジャンクションθAが準備されていて、そのジャンクションを、取 り付け演算「%」を通して自由に使ってよい圏がトレース付きモノイド圏だと 考えれば十分だろう。
クロス・ジャンクションとフィードバック・ジャンクションを組み合わせる と、図のような“結んでない輪”ができる。この結んでない輪を引っ張るとス トレートに伸びることを示す引き伸ばし公式は、特に「ヤンキング(yanking) 公式」と呼ばれる。
/* yanking */
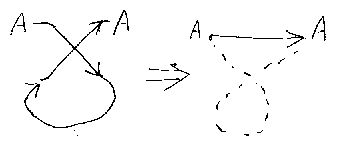
ヤンキング公式はトレース付きモノイド圏の7つの公理のひとつであり、フィー ドバック・ジャンクションに関する引き伸ばし公式だと言ってもよい(*注5)。
ヤンキング公式を、記号的表現により書き下してみれば次のようになる。
フィードバック・ジャンクションはグルリと一回転する。つまり、 方向が360度変わる。回転量を半分にしたジャンクションがターニング・ジャ ンクションである。円を左右半分にしたような形で、Uターンを行う。左でUター ンする左ターニング・ジャンクションと、右でUターンする右ターニング・ジャ ンクションがある。これらも、対称モノイド圏の対象Aでパラメータ付けられ た族であり、左ターニング・ジャンクションをηA、右ターニング・ジャン クションをεAと書く。
/* turning-junction */
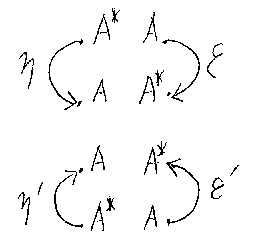
ターニング・ジャンクションは射として定義できる。が、これにはトリック が必要で、圏の対象を“反転する演算”を導入する。 対象Aを反転した 対象はA*と書く(A*はAの双対とも呼ばれる)。ターニング・ジャンクショ ンは、0→A*+A の形の射として定義される。が、0→A*+A は表向きの仕様 であって、A*→A とつながるワイヤーであり、その方向が180度回転する 「曲がった射のようなもの」と捉えるほうが実情にあっている。なお、上の図 では、矢印は“意味的な方向”を示しており、表向きの射の方向ではない。こ の“表の定義”と“裏の意味”を使い分けるには、多少の慣れが必要である。
意味的な方向が反時計回りである左ターニング・ジャンクションと共に、時 計回り方向の左ターニング・ジャンクションも導入して、これをη'Aと書 くことにする。ε'Aも同様で、意味的な回転方向が反時計回りのものである。 フォーマルには、 η'A=ηA*、ε'A=εA*と定義すればよい。
下の図を見ると、フィードバック・ジャンクションθAは、 η'AとιA*とεAを組み合わせれば出来上がるのが分かる(*注6)。実 際、ターニング・ジャンクションを使ったトレースの定義は次のようになる。
/* feedback-turning */
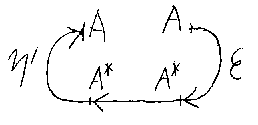
図のなかの矢印は、“裏の意味”に基づいている。恒等射A*の射としての 方向は左から右であるが、裏の意味から見ると、右から左に戻っているのであ る。
左右のターニング・ジャンクションを少しずらして向き合わせると、Z字形ま たはS字形に曲がったワイヤーが得られる。このような曲がったワイヤーは、 引き伸ばし可能である。次の引き伸ばし公式が得られる。
/* turning-stretching */
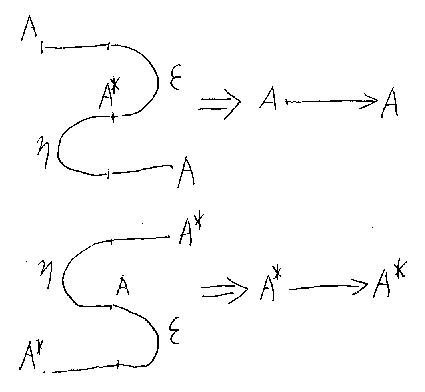
実際、Z字形、S字形ワイヤーの引き伸ばし公式は、コンパクト閉圏の主要な 公理(三角恒等式)(*注7)になっている(*注8)。
ジグザグ恒等式(zigzag identities)とも呼ぶようだ。
三角恒等式を、記号的表現により書き下してみれば次のようになる。
単なる圏から出発して、対称モノイド圏、トレース付きモノイド圏、コンパ クト閉圏という“進化”は、直線状のジャンクションから、交差や曲がり(回 転)を含んだジャンクションを取り入れる道筋だったとも解釈できるだろう。
| 種類 | 導入された基本演算 | ジャンクション | 代表的な引き伸ばし公式 |
|---|---|---|---|
| 圏 | 結合 ; | ιA | 特になし |
| 対称モノイド圏 | モノイド積 + | σA,B | 2回交差の解消 |
| トレース付きモノイド圏 | トレース Tr | θA | ヤンキング |
| コンパクト閉圏 | 双対化 * | ηA、εA | Z字、S字ワイヤーの引き伸ばし |
このなかでもっとも自由度が高いコンパクト閉圏は、トレース付きモノイド 圏の特徴を全部持っていて、かつ双対化も自由に使える。いったんは、圏に働 く(やや超越的な)オペレータとして定義されたトレースも、コンパクト閉圏 では、射として存在するジャンクションの組み合わせで表現できる。
代数的演算である「;」「+」「*」と、ジャンクションの族ι、σ、η、εを 備えたコンパクト閉圏は、かなり豊富な構造を持つと言える。一方で、演算と ジャンクションは、「直列結合、並列結合、極性反転と、基本的な各種ワイヤ リング」として素朴な解釈を許す。これらは僕が、コンパクト閉圏を“高次元 パイピング”(記事「高次元のパイピング」 参照)の背景に選んだ理由にもなっている。