/* tightening */
トレース付きモノイド圏(C, ×, 1, σ, Tr)において、 f;g≒TrYX,Z((f×g);σY,Z) を示す。
(C, ×, 1)がモノイド圏(monoidal category)で、対称(交差)σとトレー スTrを加えた(C, ×, 1, σ, Tr)がトレース付きモノイド圏(traced monoidal category)だとする。このとき、f:X→Y, g:Y→Z in Cに対して、次 が成立する(≒はisomorphic)。
これは、トレース付きモノイド圏で一般的に成立する事実として言及はされ るが、一般的には、特別に重大なことではないのかもしれない。しかし、僕に とっては非常に印象深い公式である。
というのも、この等式(同型)が成立することは、特別な状況における現象 としては1995年くらいから知っていたのである。僕が知っていた例では、対称 σの存在が分かりにくく(僕のイイカゲンな定式化のなかでは分かりにくかっ たということだが)、f;g=Tr(f×g) のように見えていた。つまり、圏の基本 演算である結合(composition)が、テンソル積(モノイド積)とトレースで 書けてしまうような形をしていた。
f;g=Tr(f×g) は、僕にとっては不可解であったし、気持ちの悪い現象だと感 じていた。なにか根本的に間違いを犯しているような不安もあった。だが、こ れはトレース付きモノイド圏が背後に存在する状況証拠だとわかって、やっと 気分が落ち着いた。
f;g≒Tr((f×g);σ)は、トレース付きモノイド圏の公理から簡単に示せるが、 簡単すぎるせいか、ハッキリとした証明が見あたらない。簡単とはいっても、 トレース付きモノイド圏に慣れてないと自明とは言えないだろう。そこで、 f;g≒Tr((f×g);σ) を具体的に示す。
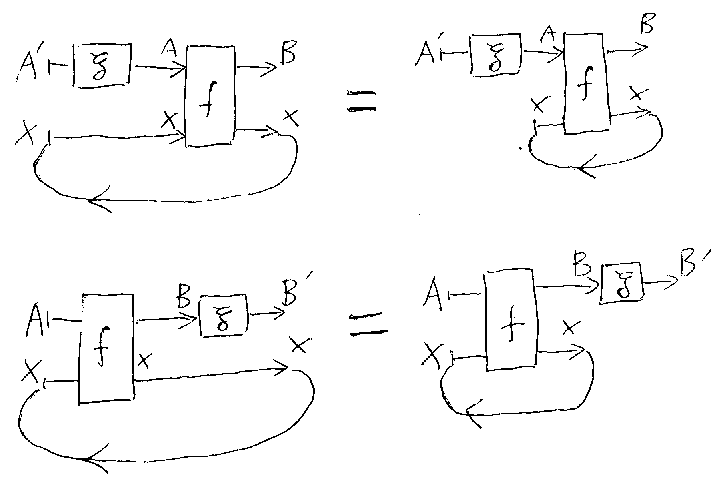
左右のタイトニング(left/right tightening)、対称(交差)σの基本性質、 「ずらし」に関しては、記事「スーパーポージング公理 からスーパーポージング定理へ」のなかに図がある。ヤンキング(yanking) の絵は、記事「お絵描き圏論」内にあ る。
念のために、図を以下に再掲しておく。
トレース付きモノイド圏の完全な定義は、Masahito Hasegawa "Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi" 1997(CiteSeer.IST を探してみよ)にある。
/* tightening */

/* cross-axioms */
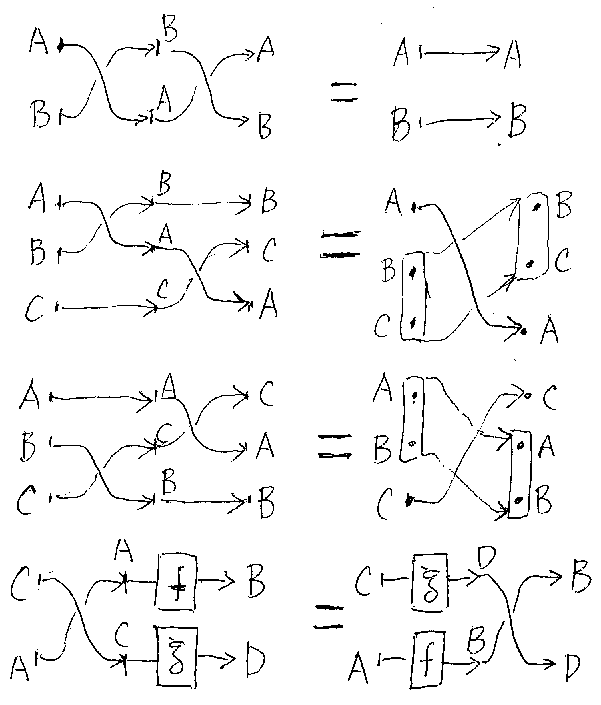
/* shift */
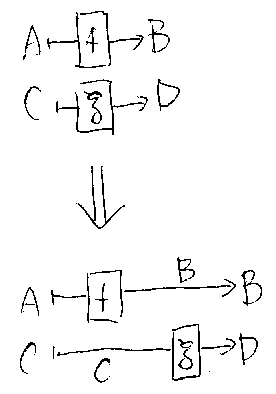
/* yanking */
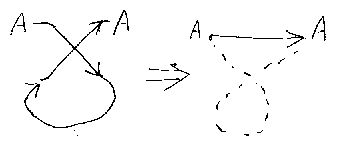
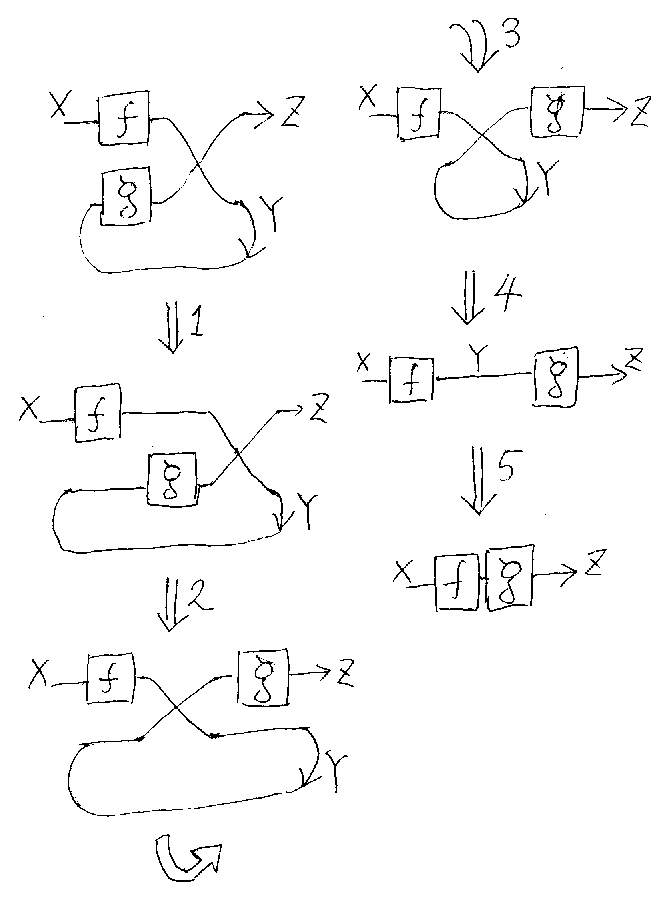
TrYX,Z((f×g);σY,Z)からはじめて、 f;gへと変形する。図式の 変形を下に描いておいた。説明は下にある。
/* composition-in-tmc */