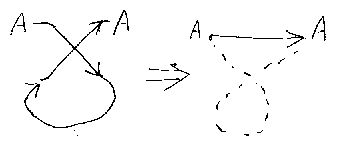
定義域を対象(objects)だけに限定した双対オペレータ(dualizer on objects)をベースにコンパクト閉圏を定義してみる。
記事「コンパクト閉圏を定義する」において、 双対付き対称モノイド圏(symmetric monoidal category with dualizer)を ベースとしてコンパクト閉圏を定義した。双対オペレータを対象(objects) だけに限定しても事情がそれほど変わらないことがわかったので、対象双対オ ペレータ(dualizer on objects)を持つ圏をベースにコンパクト閉圏を定義 してみる。
(C; +, 0, σ)を対称モノイド圏とする。圏Cの対象類|C|の上で定義された写 像(-)*:|C|→|C|が次の性質を持つとき‘対象双対オペレータ’(dualizer on objects)と呼ぶことにする。(この記事内では、同型も「=」で示す。)
対象双対オペレータが備わった対称モノイド圏を‘対象双対付き対称モノイ ド圏’(symmetric monoidal category with dualizer-on-objects)と呼び、 (C; +, 0, σ, *)のように書く。
コンパクト閉圏は、対象双対付き対称モノイド圏にKelly単位η= {ηA | A ∈|C| } とKelly余単位ε= {εA | A∈|C| } が付属した構造(C; +, 0, σ, *, η, ε)として定義する。今回の定義では、Kelly単位ηとKelly余単位εの両 方が必要である(どちらか一方から他方を定義できない)。
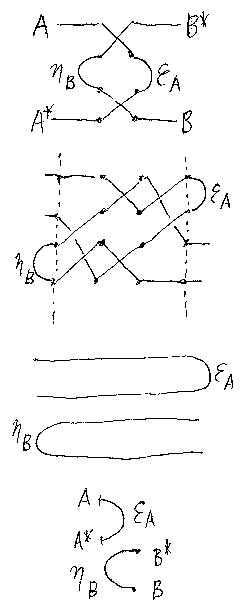
まず、A*、A + B に対してη、εがどのように振る舞うかを規定する「ねじ り公式」と「まとめ公式」を公理として採用する(これらについては、 記事「コンパクト閉圏を定義する」参照)。
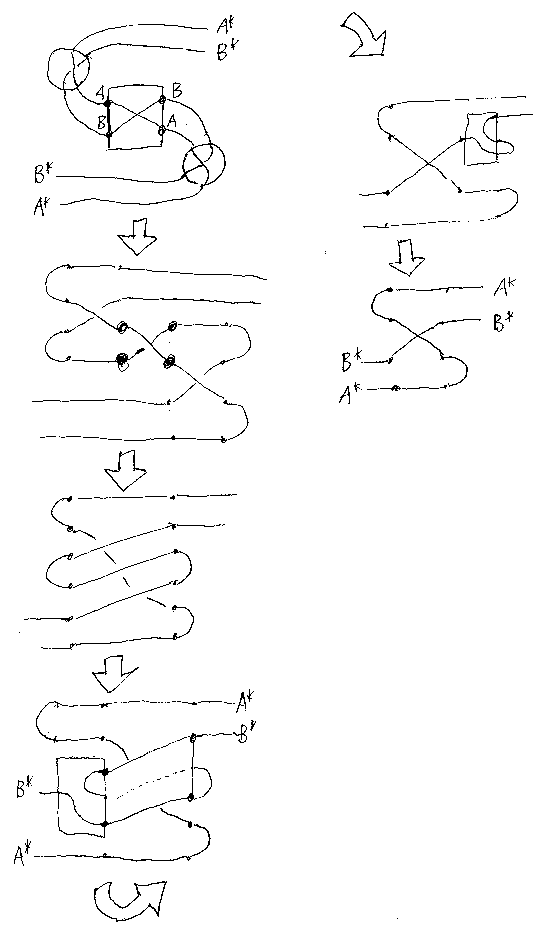
引き伸ばし公式としては、次の‘ヤンキング公式’を採用する。
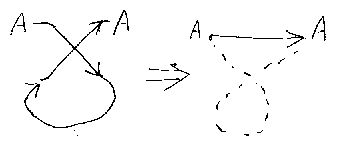
ヤンキング公式が、Z字/S字のジグザグ公式と同値であることは次のように してわかる。(以下はZ字の例だが、S字も同様である。)
よって、左ねじりを仮定すると、「ヤンキング ⇔ Z字ジグザグ」となる。同 様に、右ねじりを仮定すると、「ヤンキング ⇔ S字ジグザグ」となる。
コンパクト閉圏の通常の定義では、ジグザグだけが仮定されている。という ことは、ねじり公式やまとめ公式もジグザグから導出可能なのだろうが、僕 (檜山)はうまく導出できないでいる(なんか見落としや勘違いがあるのだろ う)。
ただし、ジグザグとヤンキングを仮定するばねじりが出ることは次のように してわかる。(この例では、S字ジグザグとヤンキングから左ねじりが示され ている。)
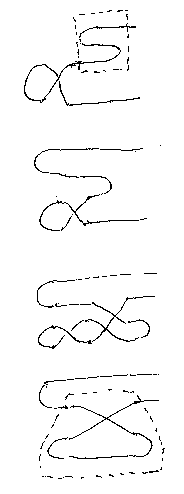
こらから、「ジグザグ、ねじり、ヤンキング」のうち2つを仮定すれば、他の1つが出てくることはわかる。
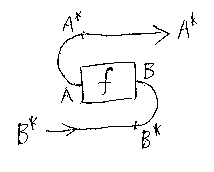
f:A→B に対して、その双対f*:B*→A*を次のように定義する。
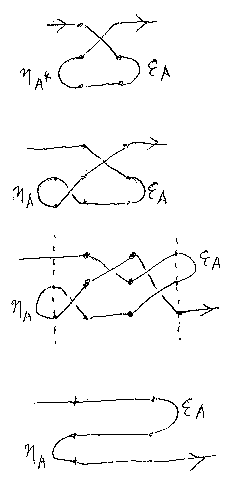
fの双対の別な表示を求めよう。 f* = (ηA* + B*);(f + σA*,B*);(εB + A*) であること が次のように示せる。
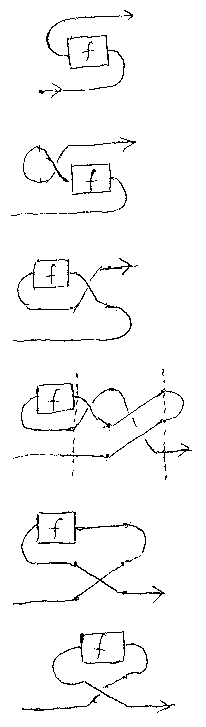
(B* + ηA*);(B* + f + A*);(εB* + A*) に関しても、左 右対称な変形操作で、(ηA* + B*);(f + σA*,B*);(εB + A*) にできるので、次の結果を得る。
以上で定義した射に関する双対には次の性質がある。
「反変関手性 2」はジグザグ公式から自明なので、他を示す。
「反変関手性 1」と「対蹠性(包合性)」は次の図からわかる(説明は省略)。
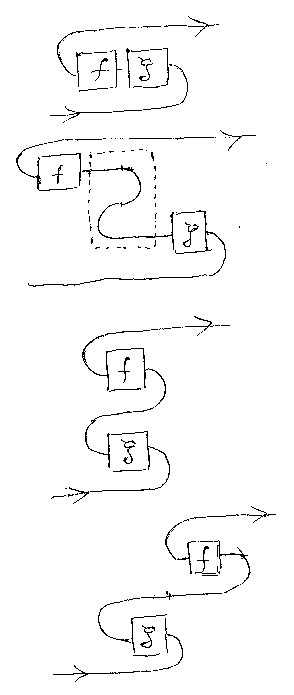
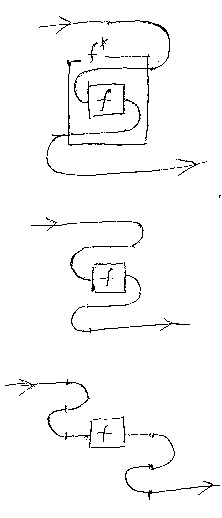
「モノイド積の保存:(f + g)* = f* + g*」を示すために、補題を準 備しておく。
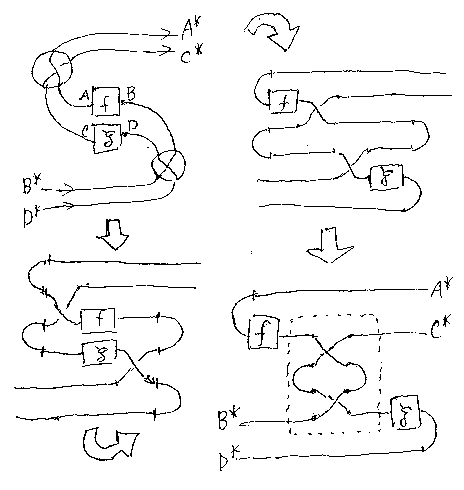
左下にσA*,0を付加して、A*とηBをスワップし、 同様に右上にσ0,B*を付加して、B*とεAをスワップする。クロスを計 算して余分なストレートジャンクションを縮めると結果を得る。
この補題を使って「モノイド積の保存: (f + g)* = f* + g*」を示す。
「対称への作用:(σA,B)* = σB*,A*」を示すために、もうひとつの補題を準備する。
常套手段を使って以下のように示せる。
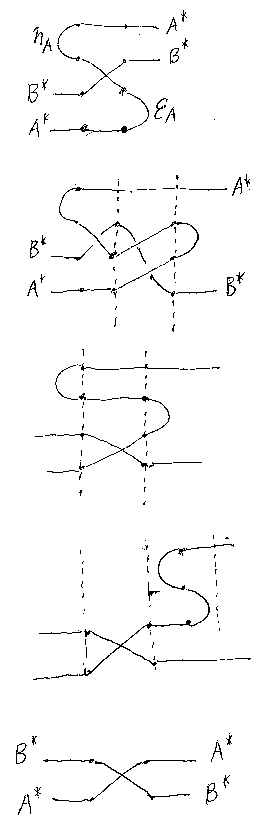
「対称への作用:(σA,B)* = σB*,A*」は次のように示せる。