/* 1 ras-as-processor */
この記事には複数の話題が含まれる(長くなりすぎた!)。
前半は「再帰代入系 1」への補足であり、後半はこれに続く記事のために基 礎を提供する。
一連の記事で、再帰代入系に関して説明しようと思っている。この説明作業 は思ったより大変であることがわかってきた。今まで僕は、状況証拠と経験と 直感により、「これはこうなるはずだ」という推測をしてきた。この推測に間 違いがあるとは思っていないが、確実な保証がないのは事実だ。
この機会に、経験と直感ではなくて、キチンと細部も詰めようと思う。それ は「たいした作業ではない」とふんでいたのだが、やってみると簡単ではない。 細部の総量はけっこうなもので、随分と手間がかかる。
しかし、キチンと保証を与えながら進まないと、僕の言っていることの根拠 は個人的な経験/個人的な直感だけのままであり、それでは(僕以外の人間は) 信じる気になれないだろう。なんだか、えらい作業量になりそうだが、それ でも僕は、すべての主張に明白な根拠を与えていこうと思う。そのぶん、先に 進む速度は遅くなるかもしれないが、それはしょうがない。
この記事は、記事「再帰代入系 1」 の続きである。以下、記事「再帰代入系 1」を単に「1」として参照引用する。
記事「1」では、再帰代入系を定義したところで息切れした。今後、引き続く 記事で再帰代入系の性質を色々と調べる必要がある。そのためにこの記事では、 「1」で説明が不十分だった点を補足した後で、置き換え (substitution)について詳しく調べる。前半のインフォーマルな説明は、形 式的な存在である再帰代入系への心理的な抵抗感を減らすのが目的だ。後半は、 多少厳密(?)に記述しているが退屈かもしれない。
まだ再帰代入系の分析には踏み込めず、そのための準備で終わっている。が、 再帰代入系は、Chimairaの構文的な議論の基礎だから、堅実に進むことにする。
この記事は分量がおおくなったので、第一部と第二部に分ける。とはいって も、区切りにそれほどの必然性はない。先(Fri Mar 04 2005)に公開した前 半が第一部、後から書き足した部分が第二部という、イイカゲンな切り方です。
記事「1」で、次のように述べた。
項とは、無意味な記号の組み合わせに過ぎない。意味を与えることはあ るかもしれないが、それはまったく別なハナシとなる。今の段階では、徹底的 に無意味である。
項が無意味な記号の組み合わせなのだから、もちろん、式も再帰代入系も無 意味である。再帰代入系のよいところは、意味に一切言及せずに、構文的 な操作だけですべての議論が行えることである。とはいいながら、無意味な記 号操作は、あまりにも味気ないので、インフォーマルには(気持ちとしては) 意味を考えたほうが(心理的に)楽だろう。そこで、再帰代入系のイ ンフォーマルな意味を説明することにする。が、あくまでインフォーマルであっ て、以下の説明の意味的内容が実際に使われることはない(*注1)。
これは、「再帰代入系に意味を割り当てることは金輪際ない」ということで はない。後で、再帰代入系の意味論を展開する。だが、そのとき、インフォー マルな説明を根拠にした議論はしない。正式な意味論はフォーマルに定義する。
まずは、代入部について説明する。代入部は、「let x=f」の形の式 (formula)の集まりである。キーワードletは、単に代入部に所属することを 示す目印である。等式「x=f」は、等しいことを意味するのではなくて、右辺 を計算した結果を左辺の変数に代入することを意味する。プログラミング言語 の代入と同じである。よって、「let x=f」の形の式は‘代入文’または‘代 入式’と呼ぶことにする。
再帰代入系の代入部において、代入文の順序は問題にならない。例えば、2つ の代入文からなる代入部は2通りの書き方があるが、これらを区別しない。 (次は例:)
したがって、代入部の“意味”は、代入文の順序に影響されない。複数の代 入文が順次実行されるのではなくて、それぞれ1回だけ同時に実行される。 もっと正確に言えば、ほんとに同時でなくてもいいが、それぞれの代入文は他 の代入文とは無関係に、入力変数の初期値のみに依存して計算を行うのである。 (と、インフォーマルには考えるとよい、ということであり、ほんとに計算や 代入を行うことが要求されてはいないので注意!)
上に挙げた例で、変数は整数値を取るとして、x=2, y=3の初期値のとき、代 入文を実行した後の結果は、x=3, y=5である。「x=x+1」の結果が、「y=x+y」 に影響することはない。(と、インフォーマルには考えるとよい。)
再帰部は、連立の再帰方程式とみなす。よって、再帰部に登場する「=」は、 「等しい」を意味しており、作業変数は「方程式の未知数」であると思ってよ い。再帰部でも、等式の記述順序はどうでもよい。再帰部の(連立)方程式の 解が、代入部の計算に使われる。
ここでもまた、再帰方程式をほんとに解くことが必要なわけではない。「再 帰部の方程式の解が、代入部の計算に使われる」かのごとくに理解すると、 理解しやすいし気持ちが落ち着くだろう、というだけである。実際、再帰代入 系の定義や再帰代入系に対するさまざまな操作において、再帰部の方程式が解 を持つことや解の一意性は全然仮定しない。
さて、 再帰部の「=」は「等しい」を意味するといったが、では、「代入の意 味はないのか?」というと、実は代入による解釈もできる。なぜなら、 再帰方程式は通常、繰り返し代入により解けるからである。「x=f(x)]という形 の方程式(不動点方程式とも呼ぶ)は、適当な値a0からはじめて、 a1=f(a0), a2=f(a1), a3=f(a2), ... という繰り返し代入の極限 が解になることがある。このような場合は、再帰部は、繰り返し代入を指示し ているとも見なせる。しつこいけど、「見なせる」だけであり、ほんとにそう だとは言ってないからね。
この節もインフォーマルな説明をする。再帰代入系のイメージをハッキリさ せるため、再帰代入系をハードウェアのごとくに考えてみる。この描像は、単 なる例え話ではなくて、モデルとしてイイ線いっている(この描像を変えずに形式 化できる)。
まず、変数のハードウェア的解釈から -- 記号的な変数とは、高水準のメモ リだと思えばよい。普通のメモリ・セルがビットやバイトを格納するのに対し て、高水準のメモリ・セルは、数学的整数や文字列や集合などを値として格納 できる。変数名がメモリ・アドレスに相当して、各メモリ・セルを一意識別す る。
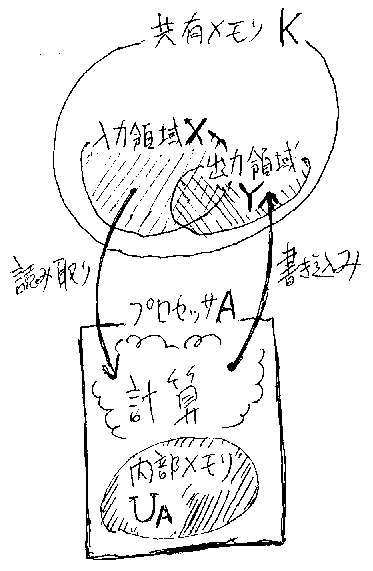
再帰代入系A=(X, Y, U, Aass、Arec)では、変数集合X, Y, Uを大き な変数集合Kの部分集合だとした(X⊆K、Y⊆K、U⊆K)。だが、変数集合Uは内 部使用するから、再帰代入系Aに固有な(プライベートな)変数集合としたほ うが実は合理的である。つまり、A=(X, Y, UA, Aass、Arec)として、 AとBが異なれば、UAとUBはまったく無関係だと考えるのである(*注2)。
再帰代入系の定式化で、U⊆Kとしているのは、作業変数集合を入出力変数と 別な領域から切り出す(アロケートする)ことにしても、他のところで面倒な ことになり、全体として労力の節約にならないからである。
さて、A=(X, Y, UA, Aass、Arec)のように考えた再帰代入系を、 一種のプライベート・メモリ付き計算装置(プロセッサ)だと考える。変数の 全体集合Kは共有メモリである。X⊆K、Y⊆Kだから、入力変数集合Xと出力変数 集合Yは、全共有メモリKの一部をプロセッサAの入出力領域として予約(宣言) している状況になる。つまり、プロセッサAは、Xから初期値を読み取り、処理 結果をYに書き込む。領域Xと領域Yが重なるのは特に問題にしない(極端な例として、X=Yでもよ い)。計算の途中では、プロセッサ固有の内部メモリUAを使う(下の図)。
/* 1 ras-as-processor */

A:X→YとB:Y→Zがあるとき、AとBの(この順での)結合(composition)A;B とは、Aを実行した後でBを実行する働きを持つ合成プロセッサのことである。 順次実行になるので、Yに格納されたAの計算結果をBが初期値(入力値)とし て使うことになる。
後(別記事)で定義するA:X→YとB:S→Tの集約(aggregation)A+Bとは、Aと Bを、まったく独立/並列に実行する働きを持つ合成プロセッサのことである。 集約を作るときは、入出力の干渉があってはいけないので、X∩SとY∩Tが空で ある必要がある。A+Bのプロファイルは、X+S→Y+Tになる(*注3)。
X∩Yが空のときは、X∪YをX+Yと表記する。現時点では、これは単なる表記上 の約束事だが、後で一般的な(圏論的な)直和「+」を導入する。
これまた後(別記事)で定義することだが、A:X+S→Y+Sに対して、AのS再帰 化(Sフィードバックとも呼ぶ)RecS(A)とは、共有メモリ領域S(のコピー) を内部メモリに取り込んでしまう操作である。SおよびSに関連した結線は内部 化されるので、RecS(A)のプロファイルは、X→Yとなる。
再帰代入系を定義するとき、変数全体の集合Kと 関数記号の集合F=(F0, F1, ...)から出発した。Kは、すべてのプロセッサ が使う共有メモリとして意味づけられるが、Fはどうだろうか。Fは、プロセッ サを作るときに使われる関数素子のレパートリである。プロセッサを作るとき、 構造の制約(再帰代入系の構成規則)はあるが、Fに属する素子は自由に使っ ていいのである。KやFを変えると、その上で作れるプロセッサの性質や能力が 変化する。だから、KとFを変化させて、その上のプロセッサの世界RAS(K, F) を考察するのも面白い問題となるわけだ。
再帰代入系の性質は、意味に言及せずに純構文的な議論だけで導き出せる。 このとき、使われる基本的な道具は、置き換え作用素(substitution operator)の性質である。
「置き換え」という訳語は一般的ではなく、通常は「(同時)代入」と呼ぶ が、この記事では、値割り当て(assignment)を「代入」と呼んでいるので、 それと区別して「置き換え」とした。
ここで、形式的体系における項とその置き換えに関する参考文献を挙げてお く。
まず、記事「形式言語理論への疑問など」の2節 で挙げておいた次の教科書。
第6章でEFS(elementary formal system)を扱っているが、ここでEFSの項、 論理式(formula)、節(clause)などが定義され、代入(substitution; 置 き換え)にも言及されている。が、詳しくは論じられていない。この本では、 代入(置き換え)を、{x1:=t1, ..., xn:=tn}という形で記している。
EFSは一種の論理プログラミング・システムであるが、論理プログラミングの 教科書である次の本では、項と代入をより詳しく調べている。
第1章第4節「解代入」が参考になる。代入(置き換え)の記法は、 {x1/t1, ..., xn/tn}で、変数と項の順序が、この記事で使っている 記法と逆である。
記事「1」の第2節で紹介した 次の本にも代入(置き換え)の記述がある。
第2章第2節で、代入、同時代入が説明されている。記号法はこの記事と同じ である(この記事が、『情報科学における論理』に従っている)。ただし、述 語論理の論理式における代入は、束縛変数があるので面倒になっている。再帰 代入系では、明示的な束縛はない。だが、作業変数が束縛変数に近い立場にあ るとは言える。
以上に挙げた参考文献/参考箇所は、置き換え(同時代入)の概念に慣れる にはいいと思うが、この記事では、これらの参考文献とは違ったやり方を採用 している。順次置き換えの展開公式 h[g/z][f/y]=h([g[f/y]/z] △ [f/y]|Zc) を示して、この展開公式を中心に据えている。
"assignment"の訳語に「代入」という言葉を使ったので、"substitution"に 対しては「置き換え」という言葉をあてた。これは、僕の個人的なこだわりみ たいなもので、assignmentもsubstitutionも区別せずに「代入」としても実害 はない。なぜなら、assignmentとsubstitutionはほとんど同義語だからだ。
再帰代入系では、代入文「let y=f」の実行が置き換え操作によりエ ミュレートされている。本来、代入は値ベースで遂行される動作だが、値の概 念を一切出さずに済ませるために記号的に実行(symbolic execution)されて いるのである。その記号的実行の手段が置き換えである。
このことは、代入部が「let y=f」であるAと、代入部が「let z =g]であるBの結合A;B(B・Aとも書く)の代入部が、 「let z=g[f/y]」という形であることからわかる。2つの同 時代入文の順次実行「let y=f; then let z=g」が、gに 置き換え[f/y]を作用させた結果g[f/y]によって記号的 に代用されている。そして、値の計算のときも、 「let y=f; then let z=g」と「let z=g[f/y]」 の実行結果(領域Zの値格納状態)は等しくなる。その意味では、置き換え=記 号的実行とは、項を値に具体化することを極力遅らせた遅延評価とも言える (*注4)。
項に意味を与えない場合は、項の具体化は行われない。つまり、評価は無限 に遅延される。つまり、純粋に構文的な計算とは、究極の遅延評価といえる。
ここまでに行ったインフォーマルな説明は、再帰代入系に親しんで欲しい/ 慣れて欲しいと思うので書いたことである。解説記事としては、そのような心 理的/教育的な効果をねらった説明は重要である。が、再帰代入系のメ リットは、いかなる意味的な支えもなしに、完全に純構文的な議論が行える点 なのである。純構文的に導き出された結論は、具体的な値領域や計算機構に依 存しないで普遍的に成立する事実/主張となる。
この「意味論独立/意味論中立」である点は、極めて強力な特性であり、再 帰代入系を何らかのデータ構造で表現したとき、それ(再帰代入系)を 扱うソフトウェアは、構文的な処理だけで普遍的な結果を出すことができる。 つまり、モジュールの実質的内容を知らずに、 モジュール操作/モジュール構成を遂行できることになる。
さらに言うと、再帰代入系は「構文独立/構文中立」だとも言える。 「純構文的な対象が、構文独立/構文中立って、そりゃなんじゃ?」というこ とになるだろうから、今は深入りしないが、再帰代入系の外部的表現方法はど うでもいい、ということだ。意味論中立で構文(外部表現)中立だと何がうれ しいかというと、非本質的で不毛な議論やら作業やらから逃れることがで きる。どうでもいい煩雑さに心底ウンザリ!している僕にとっては、これは 実に素晴らしい特徴なのだ。
ハナシが余計なことまで及んでしまった。当面の問題は“構文的な処理”と はなんだ?ということだが、構文的な処理とは、置き換え作用素 (substitution operator)の適用になる。つまり、置き換え作用素こそ、 構文的な操作/処理の実質なのである。
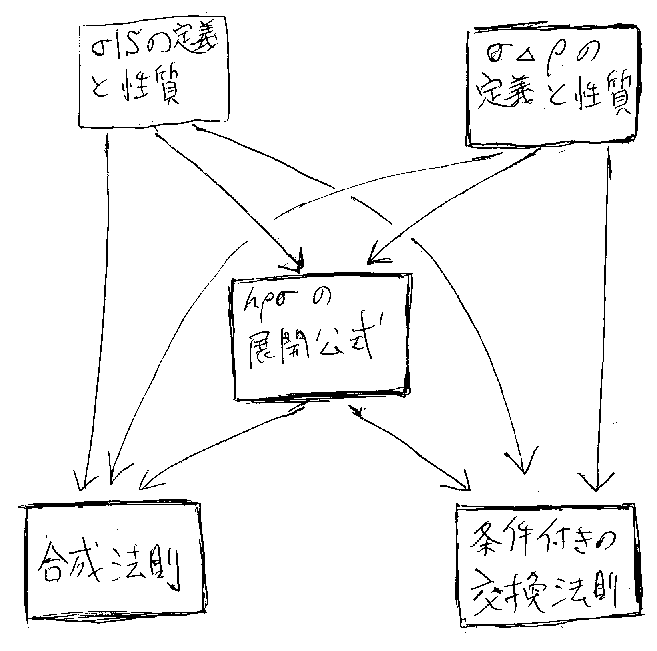
そういう事情だから、この記事のこれから後の部分では、置き換え作用素の 性質を調べる。その中心となるのは、置き換えを作用素とみた 場合の機能的な 結合(functional composition)を、構文的に実行できる演算(積、制限、和) の組み合わせで表す展開公式である。この展開公式に適当な条件を付けると、 都合がよい演算法則を得ることができる。順次置き換えの展開公式と、それに 関連する概念のあいだの関連を図に示すと次のようになる -- 第二部(次節以 降)の全体像を俯瞰するために参考にしていただきたい。
/* 2 expansion-formula */
分量的に、この記事は2本以上の記事にわけるべきだったと思うが、なりゆき 上、このまま続けることにする。この第二部は後から(Fri Mar 04 2005以降 に)書き足した部分である。
第二部の内容は、これに続く記事の基礎部分を保証するための保険のよ うなもので、特に疑義も興味もないなら、次節のダイジェストだけ読んで残り をスキップしてよい。
後半(第二部、ここから先)を読まずに済ませられるように、この節で、後半 の筋書きと概要を述べておく。
ここから先の主たる目的は、前節で触れた(順次置き換えの)展開公式を示 すことである。展開公式はけっこう強力だが、そのままの形で使うわけではな い。後で必要なのは、やはり前節で触れた(図を見よ)合成法則(2つある) と条件付き交換法則である。これらの法則だけ先に、この節で提示してしまお う。そのために、いくつか表記の約束をしておく。(これらの表記は、第二部 を通してずっと使う。)
Fは単一の集合ではなくて、F0, F1, ... と、自然数で添字付けられた集 合の族である。Fnはn引数の関数記号の集合になる。
zlの添字は、イチに見えるかも知れないがエルである。注意。
これらの記法に慣れるために、次のことが成立することを確認してみるとよ いだろう。ここで、A\B はAに含まれ、Bには含まれないメンバーの集合であ る。
適当な条件のもとで、hρσ=h(ρ*σ) が成立することを主張する定理を‘合 成法則’と呼ぶことにする。ここで「合成」は"composition"のことである (*注7)。また、適当な条件のもとで、hρσ=hσρ が成立することを主張す る定理を(条件付きの)‘交換法則’と呼ぶことにする。
通常僕は、compositionを合成でなくて結合と呼んでいる。が、用語「結合法 則(結合律)」には別な意味があるから、「合成」を使った。
ρ=[g1/z1, ..., g_l/zl]、σ=[f1/y1, ..., fm/ym]、 Z={z1, ..., zl}、Y={y1, ..., ym}だとして、次が成立する:
以上、2つの合成法則と条件付き交換法則があれば、我々に必要なことが示せ る。 これらの法則が必要になったときに、この節を見直すことにして、ここから先 をスキップしてもよい。合成法則、条件付き交換法則がにわかには信用できな い方、またはそれが成立する理由を知りたい方は続きをどうぞ。
2つの置き換えσ、ρが等しいとは何であるかをハッキリとさせるために、 置き換え[f1/y1, ..., fm/ym]を、変数の集合{y1, ..., ym}の上 で定義され、Termに値を取る写像だと考える。つまり、σが[f1/y1, ..., fm/ym]を表すとき、このσは{y1, ..., ym}→Termという写像であり、
そうすれば、2つの置き換えσ、ρが等しいとを次のように定義できる。
σが置き換えで、S⊆D(σ)だとする。このとき、σの定義域をSに制限し た置き換えを、σ|Sと書く。σ|Sを‘σのSへの制限’と呼ぶ。例えば、 σ=[f/x, g/y]、S={x}のとき、σ|S=[f/x]である。
制限に関して、次はあきらかだろう。
S⊆D(σ)のときしかσ|Sという記法を使えないのは不便である。そこで、S⊆D(σ)で ない場合でもσ|Sという書き方を使えるように、次のように定義し直そう。
これで、Sがどんな変数集合でもσ|Sが意味を持つようになった。新しい定義 によるσ|Sも‘σのSへの制限’と呼ぶ。
σは置き換え、SとTは任意の変数集合だとして、次が成立する。
制限の最初の定義も新しい定義も同じ記号「|」で表すと混乱しがちなので、 必要があれば、最初の定義を「‖」で示すことにする。また、記号が煩雑にな るのを避けるため、D(σ)をYと書く。
1番目は定義なので示すことは特にない。これは、σ|S を σ‖(Y∩S) で定 義していることになる。
2番目は次のように示せる:制限の定義より、 (σ|S)|T = (σ‖(Y∩S))|T = (σ‖(Y∩S))‖((Y∩S)∩T) となる。ここで、 ((Y∩S)∩T) ⊆ (Y∩S) ⊆ Y だから、「T⊆S⊆Yのとき、(σ‖S)‖T = σ‖T」 を使えば、(σ‖(Y∩S))‖((Y∩S)∩T)) = σ‖((Y∩S)∩T)) = σ‖(Y∩(S∩T))。 再び制限の定義を使えば、 σ‖(Y∩(S∩T)) = α|(S∩T)。 よって、(σ|S)|T = α|(S∩T)。
3番目は次のように示せる:制限の定義より、 σ|S = σ‖(Y∩S) だ が、Y⊆Sなので、Y∩S = Y である。だから、σ‖(Y∩S) = σ‖Y。さらに 「σ‖Y = σ」を使えば、σ|S = σ‖(Y∩S) = σ‖Y = σ がいえる。
4番目は、gをσで置き換えた結果と、gをσ|V(g)で置き換えた結果が等しい ことを主張している。σ=[f1/y1, ..., fm/ym]だとして、{y1, ..., ym}のなかに、gに出現しない変数yjがあれば、fj/yjは効果がないの で取り除いてもgに対する置き換えとしては変化がない。gに出現しないすべて の変数を取り除いた置き換えがσ|V(g)だから、これはgに対してはσと同じ効 果を持つ。つまり、gσ = g(σ|V(g))
σ、ρが置き換えのとき、D(σ)∩D(ρ)が空のときに限って、σ△ρという 置き換えを次のように定義する。
σ△ρをσとρの‘和’と呼ぶ。定義よりただちに次がわかる。
これらの等式は、いずれも両辺が定義できるときだけ意味を持つものである。 詳しくは記事「部分的な等号/等式」を参照。
項は、変数または関数記号(演算記号)をノードとするツリーとして絵に描 ける(例えば、記事「『形式的』とは何だろ う」の図を参照)。が、いちいち精密なツリーを描くのも面倒だから、次 のような三角形でツリーの代用とする。また、変数は必ずツリーの葉として出 現するので、三角形の底辺部分に空けた白穴によって変数を示す。
/* 3 term-diag */
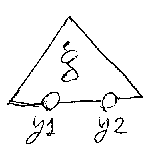
置き換えの“成分”となる変数と項の対は、次のように、項を表す三角形と 変数を表す黒丸をつないだ図形で示す。このような対をブラケットで囲んで置 き換えの図とする。
/* 4 subst-diag */
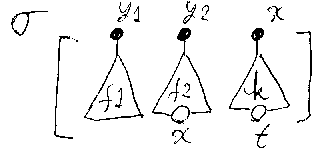
項gに対する置き換えσの適用は次のように表される。
/* 5 apply-subst */
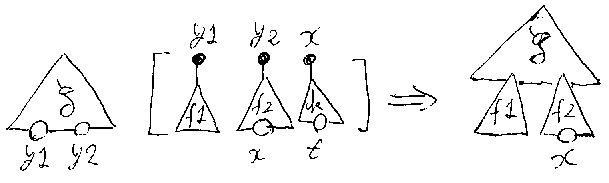
なお、項や置き換えの図は、必要に応じて向きを変えて描くかもしれない。
このような描き方で、置き換えの制限と置き換えの和の典型例を描けば、次 のようになる。
/* 6 restrict-sum-diag */
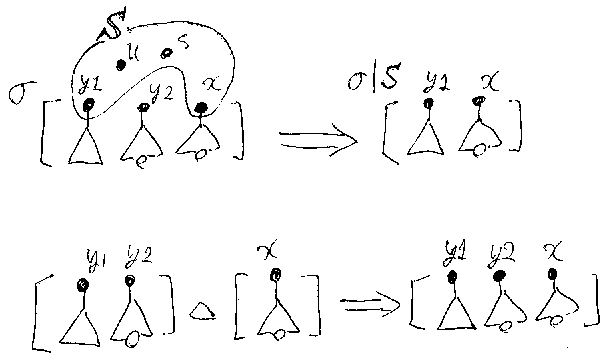
項gに対して、置き換えσを作用させた結果はgσで表すのだった。gσもまた 項である。g →gσ という対応を考えると、これは集合TermからTermへの写像 となる。この写像はσで決まるからTσと書くことにしよう。 つまり、Tσ: Term → Termであり、Tσ(g) = gσ である。
Tσ = Tρであっても、σ = ρ だとは限らない。例えば、σ=[f/x, y/y]、ρ=[f/x]だとすると、σとρは異なるが Tσ = Tρ である。これ からわかるように、「置き換えとしての等しさ」と「置き換えが定義する作用素 としての等しさ」は異なる概念である(*注8)。
置き換えσから、y/yのような置き換えとしての効果を持たない要素をすべて 取り除くことを「σを正規化する」と呼ぼう。正規化された形の置き換えは正規 形であるという。正規形の置き換えについてだけ考えれば、Tσ = Tρ から σ = ρ を導ける。かつて僕は、このことをチャント理解してなくて、 妙な間違いをおかしていた。
置き換えそのものσと置き換え作用素Tσ(置き換えが定義する作用素)を 区別した上で、次の問題を考えてみよう。
この問題に完全に答えるのが順次置き換えの展開公式である。上の条件を満 たす置き換えτは存在し、しかもτを、ρとσから積、制限、和を使って具体 的に書き下せる。次の形になる。
ここで、D(ρ)cは、変数集合D(ρ)の補集合である。
次の形に書いても同じことである。
展開公式を律儀に示そうとすると随分と面倒だから、ここでは、事例と 直感に頼った話をする。基本的な考え方を示すために、次のような典型的な実 例を挙げる。すぐ下に図がある。
/* 7 sample-settings */
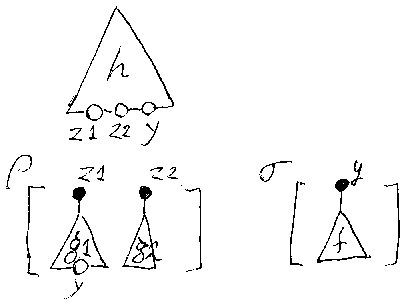
この状況で、hρσが作られる過程を図示すると次のようになる。
/* 8 sequential-apply */
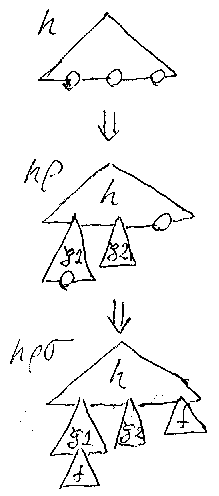
また、ρ*σ とそれがhに作用する過程は、次のように図示される。
/* 9 multiplication-apply */
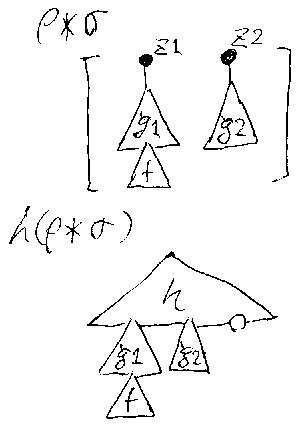
この実例では、hρσとh(ρ*σ)は一致しないが、その差は、h内に出現して いた変数yが残される点である。残された変数yも置き換えるには、もう一度σ を作用させればよいが、それは危険である。なぜなら、h(ρ*σ)のなかに「残 されたy」以外の(つまり、新しく追加された)yが出現する可能性があり、こ れを置換すると“やりすぎ”になるからだ。そもそも、仮に hρσ = h(ρ*σ)σ が成立しても何もうれしくない。
やりすぎの危険を避け、意味のある公式を得るために、“変数{y1, y2}に作 用する(ρ*σ)”と“変数{y}に作用するσ”を同時に作用させる。 これ は、(ρ*σ) △ σ となる。ただし、この例では問題にならないが、σがρの 作用に介入しないように、前もってρの作用する変数への影響を削り落として おく。その削り落としは、 D(ρ)cへの制限により行うので、σ|D(ρ)cとなるのだ 。それに、この制 限をしないと、一般的には和が定義できない。
この例から状況は理解できると思うが、少し補足しておく。ρ=[g1/z1, ..., gk/zl]、σ=[f1/y1, ..., fm/ym]とする。
これは、直感的には分かるだろうが、厳密に示そうと思うと、項に対する置 き換えの作用を構造帰納的に定義しなくてはならない。また、出現の概念の定 式化も必要である。ウーン、面倒だ!
次の「合成法則その1」を示そう。
展開公式より、 hρσ=hτ となる置き換えτがあって、そのτは次のように 書ける。
一般に hτ = h(τ|V(h)) なので、τとτ|V(h)は、hに関する作用としては 同じである。そこで、τ|V(h) を計算してみる。
(σ|D(ρ)c)|V(h) をさらに計算してみる。
ここで仮定より、V(h)⊆D(σ)なので、D(ρ)c∩V(h) は空集合になる(ベ ン図を描け)。よって、(σ|D(ρ)c)|V(h) = σ|(D(ρ)c∩V(h)) = σ|O = ε である。この結果を使うと:
結局、τ|V(h) = (ρ*σ)|V(h) である。これより、 hτ = h(τ|V(h)) = h((ρ*σ)|V(h)) = h(ρ*σ) 。 これで、合成法則その1が示せた。
展開公式から合成法則その1を示したが、展開公式を示す段階で、潜在的に合 成法則その1が使われているような気がする。よって、展開公式から合成法則 その1を示すのは、循環論法の疑いがある。
それに、直感的には(絵を描けば)合成法則その1のほうがわかりやすい。展 開公式は複雑である。複雑なことを使って簡単なことを示すのも、ちょっと妙 な感じがする。上に示した計算は、展開公式が天下りに与えられたとして、そ れから合成法則を導くときのものだといえる。
という事情で、定式化と論理展開がイマイチなのだが、まー、いいや。
次の「合成法則その2」を示そう。
合成法則その1とほとんど同じだが、同じことを繰り返し述べる。
展開公式より、 hρσ=hτ となる置き換えτがあって、そのτは次のように 書ける。
一般に hτ = h(τ|V(h)) なので、τとτ|V(h)は、hに関する作用としては 同じである。そこで、τ|V(h) を計算してみる。
(σ|D(ρ)c)|V(h) をさらに計算してみる。
ここで仮定より、D(σ)∩V(h) = O なので、 (σ|D(ρ)c)|V(h) = σ|(D(ρ)c∩V(h)) = σ|O = ε である。この結果 を使うと:
結局、τ|V(h) = (ρ*σ)|V(h) である。これより、 hτ = h(τ|V(h)) = h((ρ*σ)|V(h)) = h(ρ*σ) 。 これで、合成法則その2が示せた。
次の「条件付き交換法則」を示そう。
σ=[f/y]、ρ=[g/z]だとする。まず、ρ*σを計算しておこ う。V(ρ)∩D(σ)が空とは、V(g)∩D(σ)が空のことであり、そのとき gσ = gに注意する。
まったく同様にして、V(σ)∩D(ρ)が空のとき σ*ρ = σ である。
展開公式と上の結果を使ってρσを計算する。
ところで、D(σ)∩D(ρ)が空であることから、D(σ)∩D(ρ)c = D(σ) で ある(ベン図を描け)から、σ|D(ρ)c = σ|(D(σ)∩D(ρ)c) = σ|D(σ) = σ。これを考慮すると:
まったく同様にして、σρを計算すると:
和の性質から、ρ △ σ = σ △ ρ だから、ρσ = σρ である。
これで、後で必要となることはひととおり準備できたと思う。が、次のよう な基礎的なこと(ほとんど自明だが)は言いわすれた。
σとTσの区別について最初から言及し、区別をもっと徹底すべきだった 気がする。項と置き換えの図式も最初から導入して利用すれば、より理解が容 易になっただろう。
展開公式の根拠はあまりハッキリと示してないし、展開公式と合成法則は相 互に依存しあっている疑いもある。そもそも、置き換え作用の定義が直感的な レベルにとどまっているので、作用が登場するときに厳密な議論ができてない。
もう一度書き直せば、多少は整理した展開にできるだろうが、それは別な機 会にする(今は余裕がない)。この記事は、ブレイン・ダンプに近い文書だが、 いままで明示的には述べたことがなく、まじめに確認もしてなかった諸事実を ともかくも形にしたことでヨシとする。
いずれ、もっと厳密に述べるかもしれないが、とりあえず先に進むための足 場としては、これでも十分だろう。先に行かねば。