コンパクト閉圏における結合

• 関連記事： トレース付きモノイド圏における結合
• 関連記事： コンパクト閉圏を定義する
• 関連記事：お絵描き圏論

1. はじめに

記事「トレース 付きモノイド圏における結合」で示した f;g≒Tr^Y_X,Z((f + g);σ_Y,Z) を、コンパクト閉圏（compact closed category）のなかで確認す る。コンパクト閉圏は標準的にトレース付きモノイド圏（traced monoidal category）になるから、この公式 が成立するのは当たり前なのだが、あえて、コンパクト閉圏における変形によ り示してみる。

2. 前提

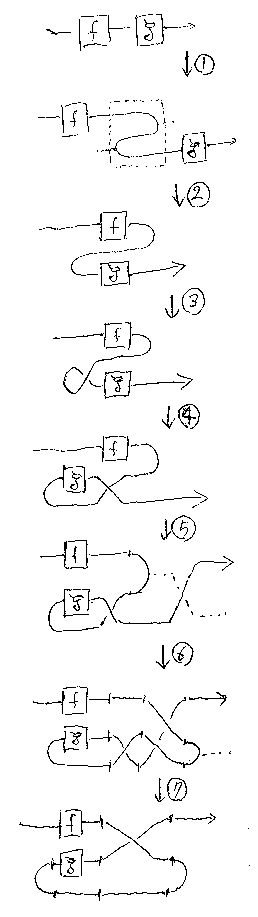
(C; +, 0, σ, (-)^*, η, ε)はコンパクト閉圏であるとする（ 「コンパクト閉 圏を定義する」を参照、εはηから定義可能）。f:X→Y、g:Y→Z がC の射だとして、それらの結合f;gをトレースで表現する。ただし、h:A+X→B+X のトレースは次で与えられる。

• Tr^X_A,B(h) = (A + η'_X);(h + X^*);(B + ε_X)

3. 図式的な証明

説明は図の後。

FIG: f;g≒Tr((f + g);σ)の証明

1. YのZ字ジグザグはY（恒等）と同じだから、YのZ字ジグザグをfとgのあい だにはさむ。
2. 位置を調整して、Kelly単位η_Y、Kelly余単位ε_Yを外側に出す。
3. 左のKelly単位η_Yをねじりを入れたη'_Y;σ_Y,Y*で置き換える。
4. Yとgをスワップして、クロス（対称ブレイディング）の位置を右に動かす。
5. 左端に、Zと0のクロスを付け加える。
6. ε_YとZをスワップして、クロスの位置を左に動かす。
7. クロスを整理して形を整える。

4. 等式的な証明

等式的な変形による証明は煩雑で鬱陶しいだけだが、念のために書いておく。 これは、図式的計算を引き写しただけであり、最初から等式的に考えたわけで はない。煩雑さ軽減するため、イコールも同型も「=」と書く。

f;g
↓f = f;Y
= f;Y;g
↓ジグザグ公式より Y = (Y + ηY);(εY + Y) 
= f;[(Y + ηY);(εY + Y)];g
↓括弧の付け替え
= [f;(Y + ηY)];[(εY + Y);g]
↓ f = f + 0, g = 0 + f 
= [(f + 0);(Y + ηY)];[(εY + Y);(0 + g)]
↓交替律
= [f;Y + 0;ηY];[εY;0 + Y;g]
↓f;Y = f, 0;ηY = ηY, εY;0 = εY, Y;g = g
= (f + ηY);(εY + g)
↓f + ηY = X;f + ηY;(Y* + Y) = (X + ηY);(f + (Y* + Y))などから
= [(X + ηY);(f + Y* + Y)];[(Y + Y* + g);(εY + Z)]
↓括弧の付け替え
= (X + ηY);[(f + Y* + Y);(Y + Y* + g)];(εY + Z)
↓交替律
= (X + ηY);(f;Y + Y*;Y* + Y;g);(εY + Z)
↓f;Y = Y, Y*;Y* = Y*, Y;g = g
= (X + ηY);(f + Y* + g);(εY + Z)
↓ ねじり公式より ηY = η'Y;σY,Y*
= (X + η'Y;σY,Y*);(f + Y* + g);(εY + Z)
↓括弧の付け替え
= [(X + η'Y;σY,Y*);(f + (Y* + g))];(εY + Z)
↓交替律
= [X;f + η'Y;σY,Y*;(Y* + g)];(εY + Z)
↓σに関するY*とgのスワップ
= [X;f + η'Y;(g + Y*);σY,Y*];(εY + Z)
↓交替律
= [(X + η'Y);(f + (g + Y*);σZ,Y*)];(εY + Z)
↓f = f;Y
= [(X + η'Y);(f;Y + (g + Y*);σZ,Y*)];(εY + Z)
↓交替律
= [(X + η'Y);(f + (g + Y*));(Y + σZ,Y*)];(εY + Z)
↓括弧の付け替え
= [(X + η'Y);(f + g + Y*)];(Y + σZ,Y*);(εY + Z)
↓ σ0,Zの追加
= [(X + η'Y);(f + g + Y*)];(Y + σZ,Y*);(εY + Z);σ0,Z;
↓ σに関するZとεYのスワップ
= [(X + η'Y);(f + g + Y*)];(Y + σZ,Y*);σY+Y*,Z;(Z + εY)
↓ σ（対称）の計算
= [(X + η'Y);(f + g + Y*)];(σY,Z + Y*);(Z + εY)
↓括弧の付け替え
= (X + η'Y);[((f + g) + Y*);(σY,Z + Y*)];(Z + εY)
↓交替律、Y*;Y* = Y*
= (X + η'Y);[(f + g);σY,Z + Y*];(Z + εY)
↓トレースの定義
= Tr((f + g);σY,Z)