ETBダイアグラム

• 関連記事：「圏論」インデックス

1. はじめに

Chimairaアーキテクチャでは、図式による説明や計算をヘビーに使うつもり だ。図式（視覚的な表現）を使えば、言葉や記号による説明／計算よりも簡便 で直感的になる（こともある）からだ。

それと、図式をベースにしたプログラミング、設計（デザイン）、コンフィ ギュレーションなどを実現したいという目論見もある。そのためには、図式法／ 図解法を明確に定義する必要がある。

と、そういうわけで、ある図式法について解説する。なお、この記事の注釈、 ノートは“読み流し／読み飛ばし”しても差しつかえない。等号の使い方に疑 問や違和感を感じたら「部分的な等号／等式」 を読むとよい。

2. 「ETB」ってなに？ 名付けた動機と経緯

この記事で紹介する図式法／図解法は、既によく使われているものである。 が、特別な名前はなくて、回路図（circuit diagram）とか単に図式（diagram） と呼ばれているようである。僕ごときが、あえてそれに名前を付けるなど、不 遜のそしりをまぬがれない行為であることは承知だ。

しかし、「回路図」では電気工学的な（本物の）回路図と区別できないし、 「図式」ではさらに漠然としている。「ベン（Venn）図」、「ハッセ（Hasse） 図」、「ファインマン（Feynman）図」などの前例にならい、人名を付けて呼ぶ のはいい方法だが、回路図は自然発生的に使われはじめたようで、創始者を特 定できない（ように思われる）。 で、おそれながら不肖檜山が命名してしまおうと -- 命名：ETBダイアグラム。

ETBは、Electronics Toy Blocksのつもりで、学研（もともとは名古屋の電子 ブロック機器製造株式会社だそうだ）の「電子ブロック」を英訳するとこんな 感じかと思って付けた名前だ。

個人的に僕は、“あのての図”（もちろん、後で説明するような図のことだ） を「LEGO」と呼んでいたのだが、LEGOは超有名なブランドだから、そのまま使 うのは問題有りだろう。ある論文では、LEGO（のようなもの）を"Brick Construction Game"と呼んでいた。例えば、テキストコードではなくて図式を 使ったプログラミングをBrick-Construction-Game style programmingとかい うわけだ。

Brick Construction Gameは長いし、略してBCGってのもどうもな^(*注1)、と 思って、代わりに"Toy Bricks"を使って、Toy Bricks diagramとかToy-Bricks style programmingとかを暫定的に使っていた（あくまで個人的にだけど）。

ある日、回路図とLEGOから、「電子ブロック」を連想した。そうだ、「電子 ブロック・ダイアグラム」ならピッタリかもしれない。これが、「ETBダイア グラム」と呼びたい理由だが、別にこの呼称を普及させたいと思っているわけ ではい。“あのての図”を、それらしい呼び名で呼びたかっただけです。なに か一般的な呼称が定着すれば、それに従います。

で、“あのての図”=“ETBダイアグラム”とは何か、次節から説明しましょ う。

3. ボックス（回路素子）とポート

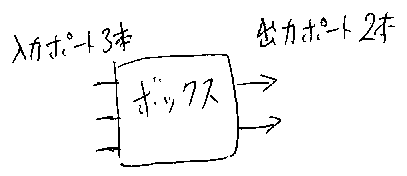
入力と出力を持ち機能を担っているナニモノカを四角い箱で表すこと にする。ここで、「入力、出力、機能とは何か」という質問は棚上げ（思考停 止）する。

箱は、‘ボックス’、‘回路素子’、‘ブロック’などと呼ばれる（この記 事では、主に「ボックス」を使う）。ボックスには、いくつか（0個でもよい） の‘入力ポート’といくつか（0個でもよい）の‘出力ポート’がある。ポー トは入力専用か出力専用で、入出力両用ポートなんてのはない。

図を描くときは、ポートは箱から飛び出した短い矢印で表す。矢の方向で、 入力か出力かを示す。だが、たとえば「左から右が入出力の方向」のような約 束があれば、矢印は適宜省略してもよい。

FIG: ポート付きボックスの例

/* box-with-ports */

ポートは、名前（ラベル）または番号で識別される。名前と番号を総称して （ポートの）‘識別子’と呼ぶ。入力ポートセットと出力ポートセットに、そ れぞれ識別子の集合が対応する。この対応（つまり、ポートの名前付け）とし ては、次の3種を考える^(*注2)。（以下で、nはポートセットに含まれるポート の本数である。n=0でポートがないときは、いずれの方式でも、空集合{}が識 別子集合となる。）

1. 整数番号：ポートセット（入力または出力）には、1からはじま る連番整数で番号を付ける。つまり、識別子の集合は{1, 2, ..., n}であ る。
2. 一意ラベル：ポートセット（入力または出力）には、互いに異なるn個 のラベルで名前を付ける。つまり、識別子の集合は {a₁, a₂, ..., a_n}である。これは集合だから、ラベルに重複はない。
3. 重複を許すラベル：ポートセット（入力または出力）には、ラベルで名前 を付けるが、ラベルが異なる必要はない。識別子のマルチセット（バッグ） は {a₁, a₂, ..., a_n}である。これはマルチセットだから、ラベルに重複 があってもよい。

同じETBダイアグラム内で、異なる名前付け方式（例えば、番号と一意ラベル） を混在させることはできない。ポートに対する名前付け方式が変わると、図式 法も別物になる^(*注3)。

識別子によるポート識別は、1つのポートセット内で行えばよい。1つの ボックスの入力ポートと出力ポートに同じ識別子が付いていてもかまわない。 また、異なるボックスで、同じ識別子を使うのも問題ない。つまり、ポートの 命名・識別は局所的なものであり、ポート識別子のスコープは、1つのポート セット（入力ポートセットまたは出力ポートセット）に局限される。

4. 直列結合と並列結合

番号によるポート識別方式を使うと話が簡単になる。よって、以下では番号 方式を仮定する。ボックスAが、n本の入力ポートを持ち、m本の出力ポートを 持つとき、A:n→m と書く。n, mは0でもよい。特に、A:0→0というボックスが 存在してもよい。0→0であるボックスは、入力も出力もないナニモノカである。

A:n→m、B:m→kがあるとき、Aの出力ポート群をそのままストレートにBの入 力ポート群につないで出来るボックスをA;Bと書き、AとBの‘直列結合’ （sequential composition）と呼ぶ。「ストレートに」とは、「Aの出力ポー ト1番をBの入力ポート1番に、Aの出力ポート2番をBの入力ポート2番に、……」 ということである。A;B:n→kとなる。

厳密に言えば、A;Bは2つのボックスの結合体であり、そのままでは1つのボッ クスではない。外側に新しく矩形を描き、全体を1つのボックスとみなしたも のが、“ボックスとしてのA;B”である。いま言ったような、「ポートをつな ぐ」、「囲いの矩形を描く」、「不要な矩形や線を消す」のようなダイアグラ ム書き換え（diagram rewriting）操作を意識することもあるが、通常は、め んどくさいのでエエカゲンに処理する。

エエカゲンに考えれば、次の等式は自明である。

• (A;B);C = A;(B;C) -- 直列結合のstrictな結合律

マジメに考えても、次は成立する。

• (A;B);C ≒ A;(B;C) -- 直列結合のweakな結合律

ここで、記号「≒」は、イコールにニョロンを乗せた記号（isomorphic）を 使いたかったのだが、見あたらないのでコレで我慢したものだ。≒の意味は、 「事実上等しいとみなせる」ってこと。≒を厳密に定義したり、≒による等式 を証明するのがマジメな態度だが、とりあえずはエンカガンな態度でいきたい。

あっ、言いわすれた。いくらエンカガンでも次のことは守ってほしい -- A;B を考えるときは、Aの出力ポート数とBの入力ポート数が同じ時に限る！出力ポー トの一部と入力ポートの一部をつなぐこともできるが、最初からそんなこと考 えるとややこしいだけだから、“完全でストレートな接続”に限定する ^(*注4)。

A:n→mとB:k→lが2つのボックスのとき、n+k→m+lであるボックスを作る。作 り方は単にボックスを並べるだけ。言葉で説明しようとすると面倒だが、絵で 描けば簡単！ 下の図を見よ。2つのボックスを並べて作ったボックスをA+Bと 書く。このA+BをAとBの‘並列結合’（parallel composition）と呼ぶ。

FIG: ボックスの並列結合

/* para-comp */

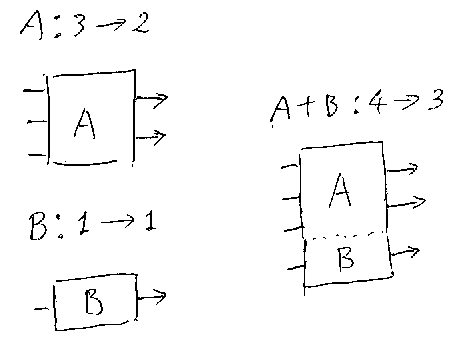
エエカゲンに考えても、A+B = B+A が成立することは保証できないから注意 せよ（しかし、適当な条件のもとでA+B≒B+Aとはなる）。演算+に関する結合 律は大丈夫だ。

• (A+B)+C = A+(B+C) -- 並列結合の結合律

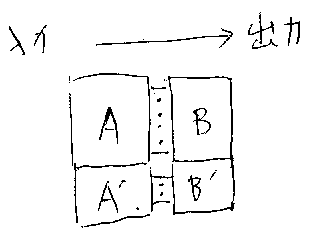
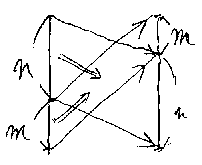
直列結合と並列結合の間には次の関係がある。

• (A+A');(B+B') = A;B + A';B' -- 交替律 (interchange law)

図を描いて考えれば、これ（交替律）も自明だろう。下のような、4つのブロッ クを組み合わせたカタマリを描いて、しばらく眺めればよい^(*注5)。

FIG: 交替律

/* interchange */

5. ワイヤーとジャンクション（接合器）

いくつかのボックスのポート間を結ぶには‘ワイヤー’を使う。ワイヤーと は、出力ポートから出て、入力ポートに入る向きが付いた線（directed edge） である。

理論上は、ワイヤーという概念は不要、というか、実は存在しない。 なぜなら、出力ポートか入力ポート（または両方）を長く伸ばせばいいだけだ からだ。とはいっても、直感的な理解や実際に絵を描くときには、ワイヤーと いう概念は便利であるから、これを使うことにする（すぐ下の「補足：ワイヤー 不要論」も参照）。

すぐ後で出てくるジャンクションは、実際にはボックスの特殊なものである。 が、図を描くときは、わざわざ箱の矩形を描かないときが多いので、結果的に ジャンクションはワイヤーとして描かれる。

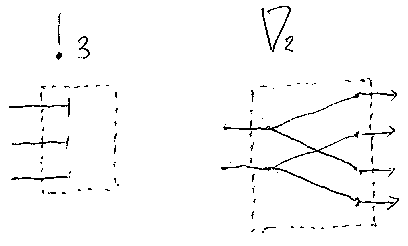
さて、‘ジャンクション’（junction; 接合器）の説明をしよう。ジャンク ションとは特殊なボックスである。記号I_n で表される自明なジャンクショ ン（あるいはストレートなジャンクション）と記号X_{n, m}で表されるクロ ス・ジャンクションを導入する。とりあえず下の図は、 I₃とX_3,2である。

FIG: I₃とX_3,2

/* I3-X3_2 */

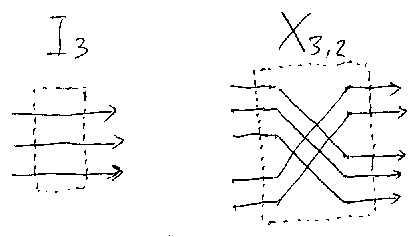
図からだいたい想像は付くと思うが、‘自明なジャンクション I_n:n→n’ は、n本の入力ボートをそのままストレートにn本の出力ポートに流すだけのボッ クスである。理論上はボックスであるが、幅がnのストレート・リボン・ワイ ヤーが適切なイメージかもしれない。I_nは、機能的にはno-operationなので、 次が成立する。

• I_n;A = A;I_m ただし、A:n→m

次に‘クロス・ジャンクション X_n,m:n+m→m+n’だが、これは幅n+mのク ロス・リボン・ワイヤーに対応する^(*注6)。これは、n+m本の入力ポートを、 {1, ..., n}、{n+1, ..., n+m}の2群に分け、前半と後半を入れ替えて出力 ポートにつなぐようなワイヤリングのことである（下図）。

FIG: クロス・ジャンクションX_n,m

/* cross */

X_1,1は2本の入力を交差させて出力につなぐ一番簡単で典型的なクロス・ ジャンクションだ。X_0,nとX_n,0は I_n のことである。

次の等式が成立する。

1. X_n,m;X_m,n = I_n+m
2. X_0,n = X_n,0 = I_n
3. X_{n, m+k}=(X_n,m + I_k);(I_m + X_n,k)
4. (A+B);X_m,l = X_n,k;(B+A) ただし、A:n→m、B:k→l

各自、図を描いて確認されたし。これらの等式から導出される法則や事実に ついては、また別に機会にする。

X_0,0 = I₀ は、入出力ポートがなくて、中身もカラッポのボックスである。 これをOと書くことにする。すると、次が成立する。

• O+A = A+O = A -- 並列結合の単位律

補足：ワイヤー不要論

ここで、ちょっと私的な話をする。僕はワイヤー概念は混乱をもたらすから、 不要というより弊害があると思っていた。ブロックの組み合わせに対応する計 算を記号的（非図形的）にするときは、ワイヤーに対応する概念はない。絵を 描く場合でも、ポートをデッパリとヘッコミで表現して、ボックスどおしをピッ タリと接合するような絵を描くことができる。

FIG: デッパリとヘッコミで表現したポート

/* wireless-box */

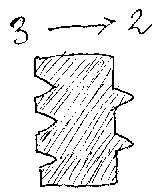
デッパリ／ヘッコミ方式なら、ほんとにLEGOのようになるし、記号的な計算 との直接的な対応も付く -- と、いいことばかりのようだが、そうではない。 ワイヤーなしで絵を描こうとすると、レイアウトが大変なのだ。注意深くブロッ クを配置しないと、うまく接合できない。その点、ワイヤーがあれば、線で結 ぶだけで接合できるからどうにでもなる。

それで結局、僕もワイヤーを描くようになったのである。そして、ワイヤー 不要論を撤回した。だがそれでもなお、あまりにもワイヤーを縦横無尽に引き 回すと、記号的計算との対応が分かりにくくなる事は警告しておきたい。

6. 放電器と重複器

一種のジャンクションとして、‘放電器!_n’と‘重複器∇_n’にも触れて おこう。放電器（discharger）は、n本の入力ポートをすべて捨ててしまうジャ ンクションである。出力はないので、!_n:n→0 である。重複器（duplicator） は、入力を2つの枝にコピーする。i番目の入力は、i番目とn+i番目の出力にそ のまま同時に出力される。よって、∇_n:n→n+nである。

FIG: !₃と∇₂

/* dis3dup2 */

次の等式が成立する。

1. !_n+m = !_n + !_m
2. !₀ = ∇₀ = O
3. ∇_n+m = (∇_n + ∇_m);(I_n + X_n,m + I_m)

さらに次も成立する。

1. ∇_n;(I_n + ∇_n) = ∇_n;(∇_n + I_n)
2. ∇_n;X_n,n = ∇_n
3. ∇_n;(I_n + !_n) = I_n

こういう等式をいきなり羅列されても、何がうれしいか分からないだろう。 そのうち、そのココロや応用を述べるつもりだが、ここで簡単な事例をいくつ か挙げておく。

事例1： 遮蔽器

m = p + q だとして、H_p,q = I_p + !_q を考える。A:n→mだとして、 AにH_p,qを後結合(post-compose)すると、A;H_p,q:n→pとなるが、定義 からAの最初のp本の出力ポートはそのままで、残りのq本は消去される。これ は出力のhiding、narrowingになる。H_p,qは、‘遮蔽器’（またはマスク） と呼んでいいだろう。より一般に、Iと!を組み合わせると、ポートセット任意 の部分集合を取り出せる。

FIG: 遮蔽器H_2,1

/* H2_1 */

事例2： n倍のコピー

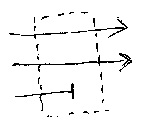
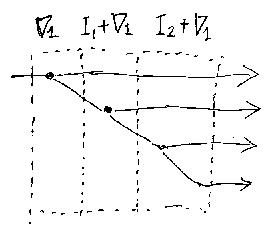
D0=!₁、D1=I₁、D2=∇₁と定義する。さらに、D3=D2;(I₁ + ∇₁)、 D4=D3:(I₂ + ∇₁)、D5=D4:(I₃ + ∇₁) のように定義していく。一般 形は、D(n+1)=Dn;(I_n-1 + ∇₁):1→n+1 である。Dnは、1本の入力を、 n本の出力にコピーして出力する。

FIG: 4倍のコピー

/* dup4 */

事例3： 自然数区間のあいだの関数の表現

f:{1, ..., m}→{1, ..., n}という関数があったとき、{1, ..., n}で定義さ れて、Pow({1, ..., m})（Powはベキ集合）に値を持つような集合値関数Φを、 逆像Φ(i)=f^-1(i)で定義する。Φは次の性質を持つ。

1. i≠j ならば Φ(i)∩Φ(j)=空
2. ∪{Φ(i)| i∈{1, ..., n}} = {1, ..., m}

このようなΦに対応するジャンクションF:n→mは、I、X、!、∇を直列結合（;） と並列結合（+）で組み合わせることによって表現できる（その表現は一意的 ではない）。fが全射であれば!は必要ない。fが単射であれば∇は必要ない。 よって、全単射なら、IとXだけを組み合わせて表現できる。fが全単射とは、 つまりはfが置換のときであり、対応するFを作用させると、ポートセットの並 べ替えとなる。

7. 参考文献ノート

対称厳密モノイド圏(symmetric strict monoidal categories)の公理（等式 群）は、 "Network Algebra with Demonic Relation Operators" J.A. Bergstra, Gh. Stefanescu の付録にまとまっている。この論文では、直列結合（射の合 成）記号は、古典的なナカマルなのだが、diagrammatic orderの意味で使われ ている。ちょっと混乱しそうだ。並列結合は、「++」に似た形の縦棒2本の記 号。feedbackは上向きの矢印を右側に付ける記法。つまり、f:m+k→n+kに対し て、f↑^k がfeedbackだ。feedbackを表す上矢印が一部ダガーになっている のは誤植だろう。identityにI、crossにXを使う記法は、この論文から拝借し た。

"The Tile Model" Fabio Gadducci, Ugo Montanari のはじめのほうにも、モ ノイド圏に関する等式が列挙されている。この著者であるイタリア（後にオラ ンダCWI）のF. Gadducciは、ドイツのAndrea Corradiniなどと共に、GSモノイ ド圏論を構築しいてる。

"Graphical Presentations of Interactive Systems" Philippa Gardnerのは じめのほう^(*注7)も参考になる。この論文では、並列結合をテンソル（記 号もテンソル積）、クロスをpermutation、traceをreflexion^(*注8)と呼んでいる。 reflexionの記号は上向きの矢印だが、左から作用させる。つまり、 t:m×k→m×l に対して、↑_m(t):k→lである。

以上の論文はいずれも、ETBダイヤグラム（と僕が呼んだ図式）を主題として 書かれたものではない。説明の都合で図式（むしろモノイド圏）に触れている だけである。図式／モノイド圏に触れている文献はおそらく大量にあるだろう。 上の3つの論文を僕が目にしたのはほとんど偶然であり、意図的に選択した結 果では全くない。もう少し調べて、その結果を 補遺に追加しようと思っている。

8. 付録：いろいろな等式

・ 直列結合

1. A:n→m, B:m→lのとき、そのときだけA;B:n→lが定義できる。
2. (A;B);C = A;(B;C) -- 結合律
3. I_n;A = A;I_m = A -- 単位律

・ 並列結合

1. 任意のA:n→m, B:k→lに対して、A+B:n+k→m+lが定義できる。
2. I_n + I_m = I_n+m -- 関手性1
3. (A+A');(B+B') = A;B + A';B' -- 関手性2、交替律
4. A+(B+C) = (A+B)+C -- 結合律
5. O+A = A+O = A -- 単位律

・ 交差器（クロス）

1. X_n,m;X_m,n=I_n+m
2. X_0,n = X_{n, 0} = I_n
3. X_{n, m+k}=(X_n,m + I_k);(I_m + X_n,k)
4. (A+B);X_m,l = X_n,k;(B+A) ただし、A:n→m、B:k→l

・ 放電器と重複器

1. !_n+m = !_n + !_m
2. !₀ = O
3. ∇_n+m = (∇_n + ∇_m);(I_n + X_n,m + I_m)
4. ∇₀ = O
5. ∇_n;(I_n + ∇_n) = ∇_n;(∇_n + I_n)
6. ∇_n;X_n,n = ∇_n
7. ∇_n;(I_n + !_n) = I_n