/* interchange */
何の断りもなく使われることが多い、部分的な等号/等式について“明示的 に”説明しておく。
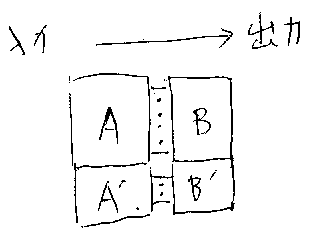
記事「ETBダイアグラム」などに、次のような等式 が出てくる(図も参照)。
/* interchange */

このとき使われている等号は、厳密に言えば、普通の等号ではない。僕は、 自分では意識せずに、したがって何の断りもなしに部分的な(partial)等号 を使ってしまった。このようなことが、理解を疎外する要因になることはおお いにありそうだ。そこで、この記事で補足説明をしたい。
例えば、交換法則(可換律)を示す等式「x+y=y+x」を考えてみよう。 この等式が表明している主張をていねいに言えば次のようになる。
ただし、この等式の前提(解釈の文脈)として、変数x, yが走る領域が決まっ ているはずだ。この領域(集合)をXとしよう。また、記号「+」で示される演 算は、X上の2項演算であるはずだ。よって、「全く任意の値」とは、Xのメン バーの範囲内での任意性である。「値は常に等しい」の“等しい”も、Xのメ ンバーとして等しいことになる。
いま、Xとして自然数(0も含める)、+は普通の足し算を考えれば、等式 「x+y=y+x」は間違いなく成立している事実である。さてここで、引き算「-」 も考えてみよう。自然数の範囲内に限定すれば、引き算はいつでも実行できる とは限らない。「x-y」が有意味であるのは、y≦xのときだけだ。この状況で 次の等式を考えてみる。
この等式は、正しい等式だといってよいと思うが、「変数x, yに、相互に独 立に全く任意の値を割り当てたとき、左辺と右辺の値は常に等しい」とまでは いえない。それよりは弱い主張で、次のような意味になるだろう。
部分的な等号でも、前の節で定義したよりは強い等号もある。たしか‘クリー ニの等号’(Kleene equality)と呼ぶのだと記憶しているが、次のような定 義である。
「(x - y) + y = x」は、左辺が意味を持たないとき(例:x=0, y=1)でも、 右辺は意味を持つから、クリーネの等号/等式ではない。
左辺や右辺に現れる式(値ではない!)をA, Bなどで表し、それが意味を持 つことを、A↓のような「地に足が着いている事を示す矢印」で表現することに する。そうすると、最初に出した 弱い等号=Weakと、クリーニの等号=Kleeneは次のように書ける。
考えてみれば、「×」を算数の掛け算として、「x×(1/x) = 1」という等式 でも、x=0のところでは左辺が未定義になる。だからこれも、弱い等式の例だ。
冒頭に出した交替律 (A+A');(B+B') = A;B + A';B' はというと、結合演算「;」 が部分的にしか定義できないので弱い等式である。次のような条件が満たされ るときしか意味を持たない。
このような弱い等式、クリーニの等式に関して、いちいち意味をもつための 条件を記述すると煩雑になる。だから、暗黙に「意味を持つときだけ考えてく ださい」という指示が入っている。けど、暗黙はいけませんね、暗黙は。