/* term-trees */
「形式的手法」、「形式言語」、「形式的体系」などの言葉には、「形式 (的)」という形容詞が登場する。この「形式的」とはどういうことなのだろ うか。主に、形式的体系について解説することによって、形式的な発想に慣れ るキッカケを提供したい。
このキマイラ・サイトや他のところの記事で僕が扱っている話題には、形式 的手法、形式言語、形式的体系など、「形式(的);formal」という形容詞が つくものが多い。同じ「形式的」という言葉でも、使われる文脈で異なる意味 あいがあるのだが、まー、共通する面もあるね。この記事では特に、「『形式 的体系』における『形式的』」について取り上げてみる。「形式的(なもの)」 に対する嫌悪感やアレルギーを取り除ければいいな、というのが僕の希望であ る。
この記事から他の記事への参照はあるが、それらの参照をたどらなくても、 この記事単独でも読める。また、他の記事に含まれる“形式的”部分に抵抗を 感じたときに読むといいかもしれない。一般教養としても、多少の意義はある だろう。
日常的な言葉の用法として、「形式的」には、「形ばかりの」、「心がこもってな い」、「内容を伴わない」といった意味がある。これじゃ印象が悪いよね。 「形式的」が嫌われるわけだよ。それに、カタカナ語「フォーマル」は、「カ ジュアル」の反対語になるから、いかにも面倒で敷居が高い感じもする。語義 矛盾は承知で言うのだが、「カジュアルなフォーマル・メソッド」が僕の目指 すところだな。
形式的手法、形式言語、形式的体系などに現れる「形式的」は、「数学や論理 学に基礎を置いた、よく定義されて曖昧性が少ない」といった意味で使ってい ると思う。が、もう少し狭く限定すると、「記号を使う」とか「記号を対象に する」ということを示してもいるだろう。特に、形式的体系とは、考察や研究 の対象としての“記号的な体系”である。
ところで僕は、「再帰代入系 1」 という記事で次のように書いた。
この記事を読むための予備知識はあまり要らないと思うが、形式的体系 (formal system)に慣れてないと辛いかもしれない。
「辛(つら)いかもしれない」と書いたのは、僕も、形式的体系に慣れてな いときに、辛い感じがしたからだ。この記事は、辛い感じからできるだけ 早く脱却する手助けになればと思って書いている。形式的な議論(formal reasoning)をうまく使えば、ソフトウェアに関する(他のことに関しても) 考察の強力な武器になる。辛い感じが薄れれば、面白さや有効性を体感できる ようになるだろう。
「再帰代入系 1」の第2節で 触れておいたが、戸田山和久さんの本『論理学をつくる』 (ISBN4-8158-0390-0) では、形式的体系を人工言語と呼んでいる。人工言語と いうほうが抵抗感が少ないかもしれない。実際、形式的体系とは、人工言語と それに関連した推論機構などを合わせた記号的システムのことである。ところ で人工言語といえば、プログラミング言語は典型的な人工言語である。だから、 形式的体系は、プログラマにとってそれほど縁遠いモノではないはずである。
一般の形式的体系がプログラミング言語と異なる点は、その目的が必ずしも アルゴリズム(処理手順)記述ではないことと、実装(言語処理系) の存在が前提にはなっていないことだろう。形式的体系は論理学やモデル論で 登場するので、実行される手順よりはむしろ、命題や主張(「××である」と いうような文)を表現するために使われる。
もっとも、プログラミング言語でも宣言文はあるし、条件のために論理式も 書ける。だから、プログラミング言語の一部として、論理的な形式的体系が埋 め込まれていると言えなくもない。一方、実在するプログラミング言語の抽象 モデルとしての形式的体系もある。実装のあるなしも確定した境界線にはなら ない。実行可能(executable)な形式的体系なんてのもあるからね。
と、そういう事情だから、形式的体系を特に恐れる必要はない。難解な印象 があるとすれば、それは、「形式的体系について説明する」という行為自体が かかえる問題点の影響が大きいと僕は思う。そこで、「形式的体系について説明 する」という行為自体がかかえる問題点について述べたい(*注1)。が、と りあえずは事例が必要であるから、次節から順次、具体的な形式的体系を定義 する。
この記事の後半で述べたい、と思ったのだが、1つの記事としては長くなりす ぎるからやめた。「形式的体系について説明する」という行為自体がかかえる 問題点は、別な記事にする(かもしれない)。
別な記事 「再帰代入系 1」の第4節で、 簡単な形式的体系を導入している。さて本記事では、変数記号集合と関数記号 集合を固定して、「再帰代入系 1」より具体的な形式的体系を1つ定義しよう。 そして、この具体的な形式的体系を事例として使う。形式的体系(人工言語シ ステム)は、項(term)と式(formula)という二種類の記号表現から構成さ れる(*注2)。まずは、項から定義する。「項」という言葉は、形式的体系に特 有の専門用語であるから、他の分野における「項」については忘れて、白紙か ら理解しなくてはならない。
項と式は、どんな形式的体系でも備えていると思う。論理を展開するには、 式の一部を公理として指定する。さらに、演繹系(証明系)も必要になる。だ が、この記事で扱う範囲では、公理や演繹系は必要ない。
項は、変数記号と関数記号の組み合わせである。ここでは、変数記号集合は {x, y}、関数記号集合としては、0引数関数記号(定数記号)が{0, 1}、2引数 関数記号が{+, *}、その他の関数記号はないとする。 「再帰代入系 1」の第4節に書 いた‘項’(term)の定義を、具体化して以下に繰り返す。
この定義に従うと、どのようなものが項になるか、その一部を 以下に列挙してみる。念のため、以下では項を引用符(「'」)でくくって示す。
関数記号(むしろ、演算記号といったほうがいいだろう)「+」や「*」が引 数の前に書かれていることに違和感があるなら、+(X, Y) → (X + Y)、*(X, Y) → (X * Y)と変換すれば次のようになる。
余分な丸括弧を取り除き、演算記号の優先順位規則(「*」は「+」より優先 する)を仮定すれば、下のように、もっと見慣れた形になる。
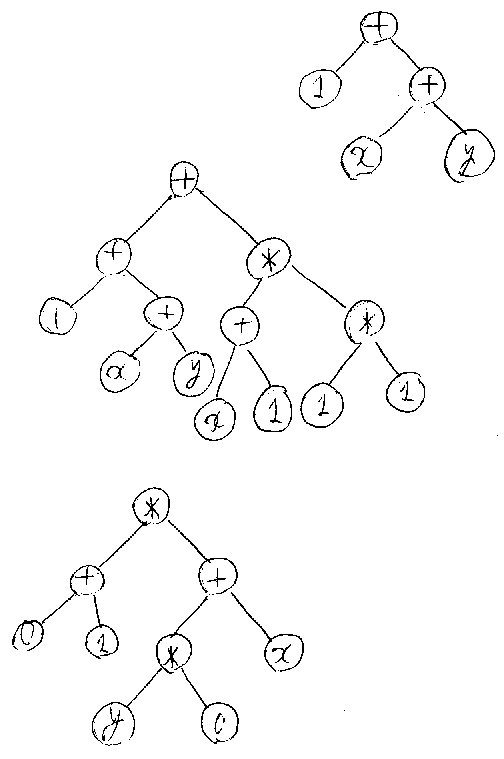
項を一列のテキストとして書く(シリアライズする)方法はいくつかあるが、 項の構造をわかりやすく表現するにはツリー図が一番だ。下の図は、3つの項 に対応するツリー図を描いたものである。
/* term-trees */

項を一列のテキストとして書けば、それは一種の文字列である。項'+(1, +(x, y))'を文字列らしく書けば、"+(1, +(x, y))"となるだろう(*注3)。また、 項をツリーだと思えば、これは一種の図形である。図形としての項をコンピュー タで扱いたいなら、グラフィックス・データとして項が定義されるだろう。(実 用上は、項をツリー状のデータ構造で表すのが便利である。)
「文字列らしく」ってのは、実は意味不明だが、多くのプログラミング言語 で文字列リテラルを二重引用符で囲む習慣があるので、それに従ってみた。も ちろん、他の書き方をする言語もあるけど。
つまり項は、文字列データ/グラフィックス・データ/ツリー構造データな どとして処理されるべきものである。ところが一方、項'+(1, 1)'を見ると、 「2という数を意味する」ような気がしてしまう。はたして、項'+(1, 1)'は2 なのだろうか? 答は「2ではない」となる。項'+(1, 1)'は項'+(1, 1)'以外の なにものでもない。
項は決して数値ではないが、「絶対に数値にはなりえないのか」 というと、実は数値になりえる。ここがややこしい! 項は単なる文字列デー タやグラフィックス・データとは、用途が違うのである。それ自体は、文字列 データやグラフィックス・データとしか言いようがないのだが、項に意味を持 たせようという下心(したごころ)が存在する。この下心の存在こそ、項が単 なる文字列データやグラフィックス・データと区別される根拠である。
下心(隠れた意図、意志)は、それが実行されるまでは認識されないし、 表立って議論の対象にもなりえない。「項には意味などない」とは、下心が実 行される以前の状態における言明である。だが、この下心がひとたび実行され てしまえば、項は意味を持つことになる。例えば、項に数値としての意味を与 える行為が実行された後では、「項は数値を表す」が真実になる。
大事なことは、項に生まれつき意味がへばりついているのではないって ことだ(*注4)。項は本来、意味的に無色であるが、「項にシカジカの意味 を持たせたい」という下心を持った連中により後から意味を付与されるの である。下心は多様であるから、同じ項に色々な意味を与えることができる。 また、項は「(いずれは)意味を持つ」ことを強要されているわけでもない。 意味を持たないままでもいいのである。
項を定義するとき、「シカジカの意味を与える予定」で項を定義することは ある。例えば、「自然数論のための項」とか。しかしその場合でも、「自然数 論のための項」に自然数以外の意味を与えることが禁止されるわけではない。 自然数を表すと信じて項を操作していても、まったく別な対象を表しているか も知れないのである。
項は意味を持つこともできるが、意味を持たないまま、項を項として操作す ることもできる。項がいかななる意味を持つかに一切言及しなくても、 項の表現である文字列/図形/木構造などを機械的に操作することはできるの だ。例えば、置き換え(代入)操作は、木の末端のノードに別な木を“接ぎ木” する操作である。
意味を持たない項を操作することは、大人にとっては辛いことだが、子供は 抵抗を感じないらしい。そのことは、記 事「遷移系と遷移翻訳系」の第1節で述べた。子供は、紙に描かれた図形を 変形する過程を、それ自体として楽しんでいるように見える。彼/彼女らは “形式的”なのだ。
記号処理が得意なプログラミング言語(例えばLisp)では、「紙に描かれた 図形を変形する過程」を、データ構造に対する操作列で容易にシミュレートで きる。つまり、子供が行っている記号的かつアルゴリズム的な行為を、コンピュー タにやらせることができる。大人は「無意味な操作を無心に遂行する」ことは もはや無理だから、大人が形式的になるためには、記号処理プログラムを書く ような、メタな立場からの理解しかないのかもしれない。
ただし僕は、(大人の)記号操作は意味に支えられているという仮説もあま り信じてはいない。最初は無意味だった記号操作も、それをたくさん経験する うちに、「背後に意味がある」という幻想を引き起こすだけかもしれない。そ もそも、記号操作行為が意味に支えられているのか、機械的アルゴリズムに 従っているだけなのか、それを判定する方法がない。
前節で述べたように、項に“生まれつき備わった意味”などない! だが、後 から意味を割り当てることはできる。この節で、項にいくつかの意味を与えて みる。
自然数とは非負の(つまり、0も含む)整数である。変数(我々の例では、 'x'と'y'だけ)が“走る”領域として、自然数の集合{0, 1, 2, ...}を採用す る。古典的な言い方では、「変数x,yの変域は自然数の集合である」となる。
ここで注意:次のような疑問を感じなかっただろうか -- 「上の段落内に登 場する'0'、'1'、'2'などは何なんだ?」「これらも単なる記号ではないか。 単なる記号が自然数を表す根拠はいったいなんだ?」 -- いい指摘だ。が、こ れを気にしはじめると、記号の意味を確定するための無限後退の過程に陥る。 僕(檜山)が、通常の日本語で書いた“地の文”のなかに登場する記号は、常 識により解釈して欲しい。僕は、この記事を、決して形式的に書いているわけ ではない。僕が普通に書く'0'は、無意味な記号ではなくて、整数のゼロであり、 ゼロの概念はあなたが常識的に知っている「あのゼロ」である。
説明を続ける。項の意味を次のように定める。
以上の説明を読んで、「なにを、あたりまえのことを繰り返し言っているん だ?」と思ったかもしれない。そんな感じがするのは、 記号'0', '1', '+', '*'などが、既に常識的な意味を持っているからである。 「意味などない」と僕が強調しても、あなたは見慣れた記号の意味を無意識に 前提にしている。だから、新たに定義したことを「既に知られていることを、 繰り返し述べている」と捉えてしまうのである。
納得がいかないなら、他の意味付与の例を見ていただきたい。それほど、あ たりまえではないはずである。
変数の変域は、真偽値の集合{true, false}とする。
この解釈では、項'+(1, 1)'は自然数2を意味しない。(true and true)だから、 '+(1, 1)'はtrueを意味する。この解釈では、項'1 + (x + 1)'は、x → x+2 という関数を定義しない。xがなんであれ(つまり、xがtrueでもfalseでも) 項'1 + (x + 1)'の値はtrueになる。
Pは、0以上の実数の集合だとする。つまり、P={x | x≧0である実数}。Pの値に 対してPの値を対応させる関数の全体をFとする(*注5)。つまり、f∈Fとは、fが非負 実数の上で定義された非負実数値の関数であることだ。
すべての関数を考えるのが嫌なら、連続関数とか多項式関数に限定してもよ い。0を0に移す増加関数(単調関数)なんかが扱いやすいかもしれない。
変数の変域は、関数の集合Fとする。
変数の変域は、例1と同じく自然数の集合{0, 1, 2, ...}である。
この解釈では、項'+(0, 1)'の意味(値)は0である。項'+(0, x)'の意味(値) は、変数'x'に与えた値と同じになるが、これは、等式 +(0, x) = x が成立し ていると考えてよいことになる。また、項'*(1, x)'の意味(値)は、変数'x' に与えた値と同じになるが、これは、等式 *(1, x) = x が成立していると考 えてよいことになる(*注6)。
この例は、記号と意味の対応がエキゾチックだが、それほど変なものではな く、系統的な計算が遂行できる体系である。
変数の変域は、文字'a'、'b'から作られた列の集合(つまり言語)の集合と する。つまり変数は、言語を表すことになる。言語とは列の集合であり、列を 構成するアトムは文字'a'、'b'となる。
この例の項は、言語の繰り返し(Kleeneスター演算)を除いた正規表現にな る(繰り返しがないと、正規表現とは呼ばないかもしれないが)。
すでにここまでで、形式的体系について説明するときの困難の一部が現れて いる。例1で、「1の意味は1である」というたぐいの文がある。もちろん、て いねいに言えば、「'1'という記号(あるいは図形)の意味は自然数値の1であ る」となる。一方、例4では「1の意味は0である」となっている。これもてい ねいに言えば、「'1'という記号(あるいは図形)の意味は自然数値の0である」 となる。
一般に、「Xの意味はYである」というとき、Xは記号や記号的な図形であり、 Yはなんらかの実体である。ところが、実体(抽象的な存在物かもしれない) を指し示すために使われる記号が見慣れたものだととかえって混乱する。たと えば、「赤の意味は赤である」と聞けば、「何を当たり前のことを」と思うだ ろうし、「赤の意味は青である」と聞けば、「何をバカなことを」と思うだろ う。だから、形式的体系に意味を付与する説明文は、往々にして「当たり前」 か「バカ」なことを言っている文に思えてしまう。
項は、下心としては、値やモノを表すつもりの記号的表現であった。それに 対して式(formula)は、「××である」という命題ないしは主張を表現する ためのものである。もちろん、主張を表現したいという希望もあくまで下心で あり、最初から式に主張が含まれているわけではない。項と同様に、式もある 種の文字列や図形として定義され、必要があれば後から意味を付与する。
「式」も形式的体系に固有の専門用語であり、他の分野(あるいは日常的な) 「式」とは別物である。普通は、記号的な表現を何でも式と呼ぶが、形式的体系にお ける式は、項とは区別される記号的な表現である。
式を定義するには、述語記号とか関係記号とか呼ばれる記号を新たに導入す るが、ここでは、等号「=」だけを使うことにする。今まで出てきた 記号達、'x', 'y', '0', '1', '+', '*' に加えて、'='も使ってよいとする。
さて、‘式’の具体的な定義は次のとおり。
等号「=」が前にあるのが嫌なら、'(t1=t2)' と書いてもよい。 これは、項' +(X, Y)'の代わりに'(X + Y)'と書くのと同じことである。以下 では、等号を中置した'(t1=t2)'を使うことにして、まぎれがないなら括 弧をはずした't1=t2'でもよいとしよう。
今考えている事例では、式は等式だけである。等式の意味は、「左辺と右辺 が等しい」と定義したいだろうが、前もってそう決まっているわけではない。 等号、つまり横二本棒の図形が何を意味するかは、意味を付与する者が自由に 決めてよい(*注7)。
横二本棒の図形が「等しい」を意味する必然性は何もない。だが、世間には 習慣というものがある。つまり、ほとんどの場合、等号は実際に等しいことを 意味するのだ。
以下では、見やすくなるように、関数(演算)記号も等号も中置で書くこと にする。つまり、'+(1, 0)'は'(1 + 0)'と書き、'=(1, 0)'は'1=0'と書くこと にする。
'(1 + 1)'と'1'は項であるから、式の定義から、'(1 + 1)=1'は式となる。さ て、式'(1 + 1)=1'は正しいだろうか? -- もうお分かりと思うが、この質問 自体が曖昧/不正確である。なぜなら、項と式の解釈を特定してないからであ る。
第6節で、意味付与の例を5つ挙げた。
項と式に意味を付与するためのメカニズム全体をまとめて‘モデル’と呼ぶ。 この「モデル」という用語も形式的体系やモデル論特有の用語であり、他分野 で使われている言葉「モデル」とは区別するべきである。
第6節では、5つのモデルを示したことになる。これらのモデルにより項に意 味を付与したが、式の意味はまだ定まってない。以下では、記号「=」の意味 を、常識に従い「等しい」ことだと解釈することにする。そうすれば、式に意 味を与えることができる。
式が正しいかどうかは、モデルに対して相対的である。実はこれは、プログ ラムが正しいかどうかが仕様に対して相対的なのと事情が同じである。事情が 似てるのではなくて、事情がまったく同じなのである。形式的体系とモデル論 が、プログラムと仕様の考察に利用できる理由がここにある(*注8)。
僕が、XMLの構文論と同等に、プログラムの仕様や検証に興味を持つのは、興 味が発散しているわけでもなく、単なる偶然でもない。要するに同じ対象だか ら、同じように興味がある。2つ(あるいはそれ以上の)の領域に興味がある のではなくて、僕にとっては単一の対象/領域である。
それはともかく、式'(1 + 1)=1'が、5つのモデルに対して正しいかどうかを 見てみよう。
左辺'(1 + 1)'は自然数2を意味する。右辺'1'は自然数1を意味する。 左辺と右辺は等しくない。よって、式'(1 + 1)=1'は正しくない。
左辺'(1 + 1)'は真偽値trueを意味する。右辺'1'は真偽値trueを意味する。 左辺と右辺は等しい。よって、式'(1 + 1)=1'は正しい。
左辺'(1 + 1)'は関数 x→2x を意味する。右辺'1'は関数 x→x を意味する。 左辺と右辺は(関数として)等しくない。よって、式'(1 + 1)=1'は正しくな い。
左辺'(1 + 1)'は自然数0を意味する。右辺'1'は自然数0を意味する。 左辺と右辺は等しい。よって、式'(1 + 1)=1'は正しい。
左辺'(1 + 1)'は言語{ε}を意味する。右辺'1'は言語{ε}を意味する。 左辺と右辺は等しい。よって、式'(1 + 1)=1'は正しい。
当然ながら、式の正しさはモデルの選び方によって色々と変わる。が、モデ ルを特定すれば、変数を含まない式の正しさを判定できる。では、変数を含む 式の正しさはどう考えたらよいだろうか。例えば、 式'(x * y)=(y * x)'は正しいかどうか、という問題にどう答えるか、である。
1つの考え方は、「変数を含む式については正しさを考えない」というもので ある。この考え方を採用するケースが多いのだが、我々は別な考え方をしたい。 つまり、変数を含む式についても正しさを考えたい。次のように考えよう。
例えば、先に出した例'(x * y)=(y * x)'を、真偽値モデルで考えると、 変数'x'と'y'に代入できる値の組み合わせは全部で4種類である。
これらのそれぞれの場合に、左辺'(x * y)'の値と右辺'(y * x)'の値を求め ることができる。記号「*」の解釈はand演算である。実際にやってみれば、 どのケースでも左辺の値と右辺の値が等しい。よって、 変数を含む式'(x * y)=(y * x)'は、真偽値モデルにおいては正しいと判断で きる。
ただし、モデルの領域(変数の変域)が無限であるときは、「どんな値を代 入しても正しい」かどうかの判断のために、しらみつぶしに全部調べることが できない。だから、変数を含む式の正しさは、いつでも確認できるという保証 がないのである。保証ができないなら、それは「正しさの定義」とは呼べない のではないか、という疑念は考慮すべき正統な意見だが、話がややこしくなる から今は議論しない。
この記事の事例では、式は単純な等式に限られる。だから、式の正しさを“変 数を含まない式”に対してしか定義しないと、ちょっと表現力が乏しくなる。通常 の(述語論理の)形式的体系では、∀(「すべての」を意味する)や∃(「存 在する」を意味する)という限量子が入っているので、'(x * y)=(y * x)'と いう変数が入った式の代わりに、'∀y.∀x.(x * y)=(y * x)'という式を使え る。限量子'∀'を使えば、本文で述べたのと同等な正しさを定義できる。
限量子'∀'を付けた'∀y.∀x.(x * y)=(y * x)'という式は、変数を含んだ式 とは考えない。見た目の上で出現している'x'、'y'は、'∀y.∀x.'に“縛られ ている”ので、変数(正確には自由変数)とは考えないのである。
だが、モデルの領域が無限のとき、しらみつぶしが使えないという問題は、 限量子'∀'を導入しても何ら改善しないことは注意しておく。 '∀y.∀x.(x * y)=(y * x)'が正しいと主張するためには、 結局は'(x * y)=(y * x)'の正しさを確認する必要がある。
僕は、「形式的体系について説明する」という行為自体がかかえる問題点に ついて述べよう、と思ってこの記事を書き始めたのだが、その話題よりは、簡 単な形式的体系を実際に構成してみる話になってしまった。だが、それでも、 形式的体系に対するアレルギー除去の役には立つだろう。
この記事で取り上げた、1つの具体的な形式的体系について考えてみれば、形 式的体系が何であるかのおおよそのイメージはつかめるだろうし、記号と意味 が混乱しがちであること(それが、説明のさいの困難の原因)も察しがつくと 思う。
形式的体系についての説明や学習につきまとう困難を知らずに、形式的体系 に慣れてしまえるなら、それは実にハッピーなことだから、「困難はここだ」と いう指摘が建設的かどうかは疑わしい。よって、「形式的体系について説明す る」という行為自体がかかえる問題点について述べる記事がほんとに書かれる かどうかも疑わしい。
なにはともあれ、ここでこの記事はオシマイです。多少は、「形式的(なも の)」に対して親しみが持てたでしょうか。