Int（GoI）構成

檜山正幸 (HIYAMA Masayuki)
Fri Jul 21 2006:start
Fri Jul 21 2006:draft

トレース付き対称モノイド圏CからInt構成（GoI構成）により圏Gを作る。 構成したGが実際に圏であることを確認する。

目次

1. はじめに

C = (C; +, 0, σ, Tr)がトレース付き対称モノイド圏のとき、標準的な方法 でCからコンパクト閉圏Gを構成できる。CからGを作る構成はInt構成、ま たはGoI（Geometry of Interaction）構成と呼ばれる。CからInt（GoI） 構成で得られた圏をInt(C)、またはG(C)と書く。

この記事では、G = Int(C) = G(C) が圏であることだけを確認する。実 際にGがコンパクト閉であることや、CをGに埋め込めることなどは別な記事 で示す。Int構成の基本的なことも述べてないので（それも機会があれば解説 するつもりだが）セルフコンテインドにはなっていない。

NOTE: 図式の簡略化

この記事に出てくる図式はやや煩雑である。その主な原因は、クロスの計算 （対称群の計算）が頻繁に登場するからだろう。この記事をほぼ書き終えた後 で、クロスの計算とトレースを整理した形の図式法を思いついた。もし、新し い図式法が有効なことが確認できれば、この記事の内容も新図式法で書き換え るかもしれない。

2. Gにおける結合

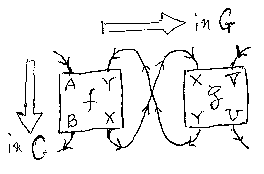
アブ ラムスキーなどは、圏Gにおける射の結合（composition）を次のような図 で表現している。

FIG: 圏Gにおける結合：対話的結合

この図において、ボックスで表現されている射は、圏Cにおける射f:A+Y→B+X、 g:X+V→Y+U であるが、圏Gでは、f:(A, B)→(X, Y)、g:(X, Y)→(U, V) と解 釈する。Gにおける射の向きは、この図では左から右になる。対(A, B), (X, Y)（対の成分はCの対象）は、域（domain；左側）では上から下に“Aの下にB”、 余域（codomain；右側）では逆に“Yの下にX”のように描かれる。同じボックス を圏Cの射として読みたいときは、上から下に向かって見ればよい。

圏Gにおける結合を対話的結合と呼ぶ。対話的結合は次のように単純化し て描いてもいいだろう。波線が対話的結合（圏Gにおける結合）を表現してい る。

FIG: 単純化した対話的結合

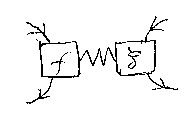
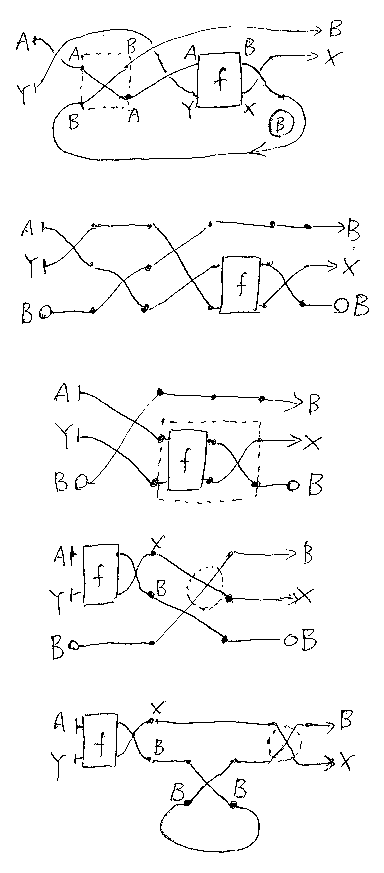
圏Gにおける結合（対話的結合）は、最初の図に示したように“たすきがけ” にワイヤーを繋ぐことになる。これを圏Cで表現すると次の図のようになる。 g# = σ;g;σ と定義したg# を使うと配線が少し簡明になる -- 下側はg#を使って描いた図である。

FIG: 圏Cにおける対話的結合の表現

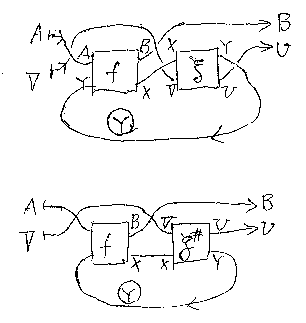
“たすきがけ”のためにはトレース（図で、TrYによるループはYに丸印 で表している）が必要となる。fとgの対話的結合（つまり圏Gにおける結合） を★とすると、次のように表現できる。

トレースの被演算項は、(V + f);(σV,B + X);(B + g#) としてもよ い（左タイトニングから）。

この表現は、対称性が欠けているので、双対をうまく利用できない欠点があ るのだが、“たすきがけ”を素直に表している点がメリットなので、この表現 により議論を進める。

NOTE: 対称を少なくした表現

上に挙げた対話的結合の表現では、対称が4回出現する。対称の数をもっと少 なくすることができる。縄跳びの補題により、V ワイヤーを下にさげて、中間に集まった対称を整理すると次の形になる。Yの 両端が丸印になっているのは、トレースを取ることを示す。

FIG: 対称を少なくした表現

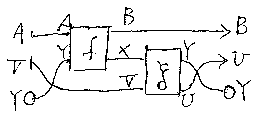
この表現を使うほうが、対称が少ない分、計算が楽になるだろう。

3. 圏Gの記述

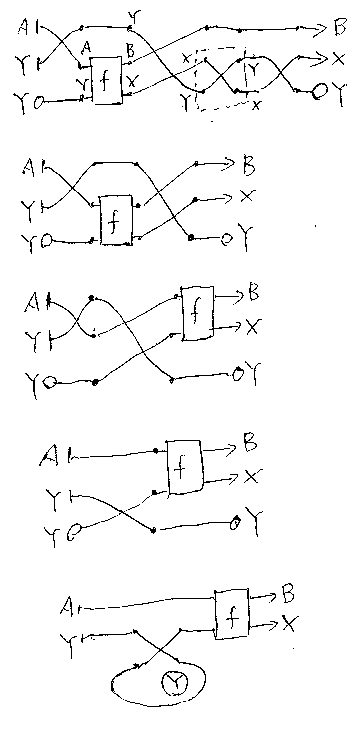
A, Bなどは圏Cの対象、(A, B)などは圏Cの対象の対で、圏Gの対象である。圏 Cにおける射f:A+Y→B+XをGの射f:(A, B)→(X, Y)と考える。以下の図は、Gの射を Cで考えやすいように描いたものである。 必要に応じて参照するとよい。

FIG: Gの射をCで考えると

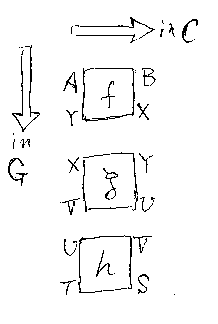
Gの対象(A, B)に対して、その（Gにおける）恒等id(A, B)は、Cにおける 対称σA, B:A+B→B+A によって与えられる。よって、Gが対話的結合に関 して圏であることを確認するには、Cで次の等式（実際には同型）を示せばよい。

4. 対話的結合の結合律

結合律を示すために、(f★g)★h と f★(g★h) を別々に計算して、一致する ことを確認する。以下に図で、ワイヤーの端が丸印のものは、後でトレースを 取る（ループさせる）部分である。

FIG: 結合律 1
  1. 定義に従って(f★g)★hを描く。点線で囲まれた部分が(f★g)である。
  2. Xに関するトレースとVに関するトレースを、タイトニングとバニッシング を使って、まとめて外に出す。トレースの被演算項だけを図に描く。
  3. g#をもとに戻す。
  4. クロスを計算する。
  5. VとFをクロスに沿ってスワップする。
  6. クロスを計算する。
FIG: 結合律 2
  1. 定義に従ってf★(g★h)を描く。点線で囲まれた部分は(g★h)#である。
  2. トレースを外に出して、トレースの被演算項だけを図に描く。クロスを 計算する。
  3. VとYのクロスを両端に挿入（丸で囲ったところ）。これらはスライディングで消える。
  4. h#とYをクロスに沿ってスワップする。gは左にずらしておく。
  5. クロスを計算する。

5. 対話的結合の単位律

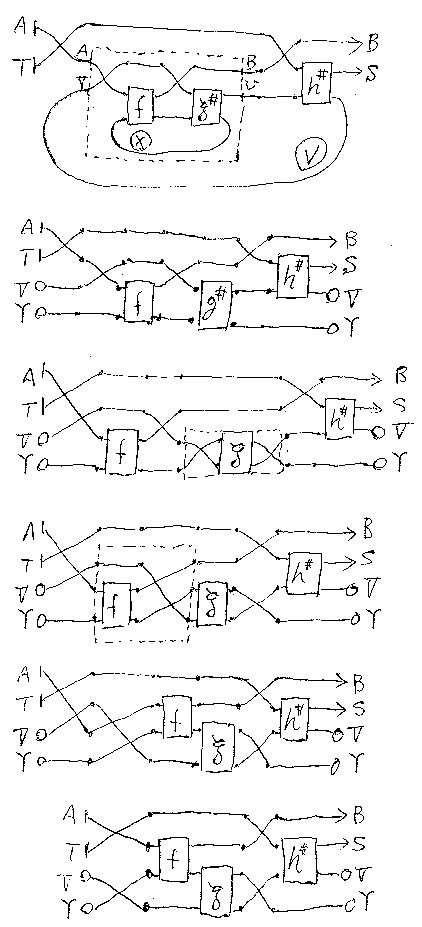
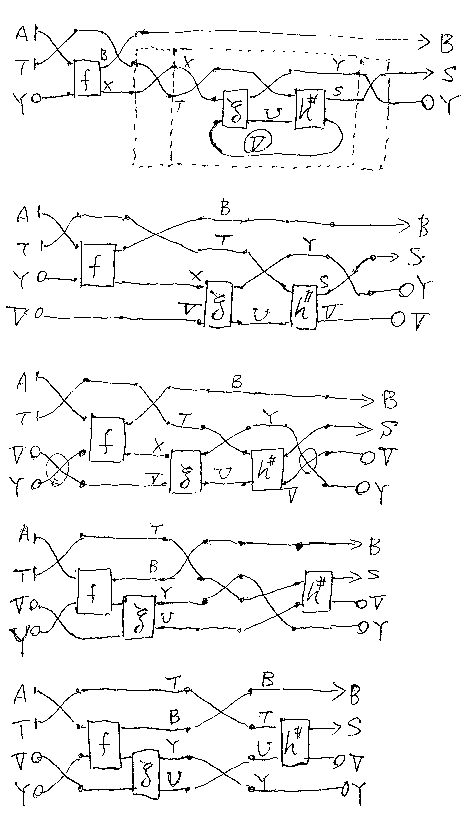
定義に対称性がないので、右単位律と左単位律がまったく同じというわけにはいかない。

FIG: 左単位律
  1. 定義に従って、σA,Bをfに左結合する。
  2. トレースを外に出して、トレースの被演算項だけを図に描く。
  3. クロスを計算する。
  4. Bとf;σをクロスに沿ってスワップする。
  5. XとBのクロスを右にずらす。
  6. Bのヤンキングができるから、これを伸ばして、クロスを相殺する。
FIG: 右単位律
  1. 定義に従って、σA,Bをfに右結合する。トレースの被演算項だけを図に描いている。
  2. クロスを計算する。
  3. Yとfをクロスに沿ってスワップする。
  4. クロスを計算する。
  5. Yのヤンキングができるから、これを伸ばす。