/* superposing */
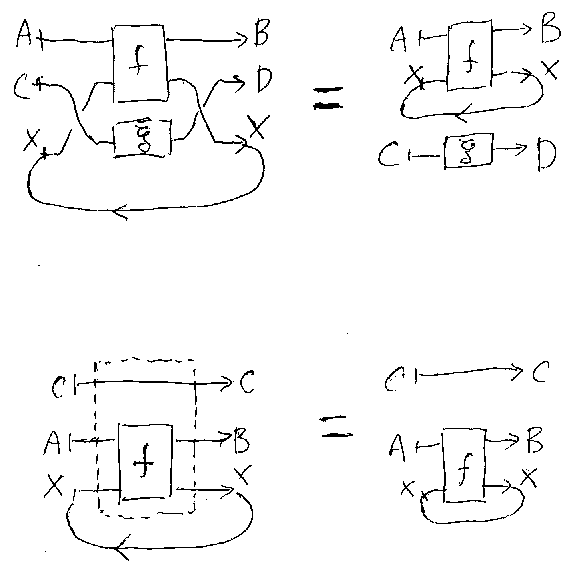
JSV96における“トレース付きモノイド圏のスーパーポージング公理”を、簡 略化されたスーパーポージング公理(それを「垂直タイトニング公理」と呼ぶ ことにする)から導いてみる。
この記事は、トレース付きモノイド圏(traced monoidal categories)のスー パーポージング公理(the Superposing axiom)に関する注意と解説である。
しばしば「JSV96」と称される、A. Joyal, R. Street, D. Verityの論文 "Traced monoidal categories" 1996 では、スーパーポージング公理が次の形 で与えられている(*注1)。( 下の図を参照。なお、記号と表記法、図の描き方などは次の節で説明 している。)
JSV96は、トレース付きモノイド圏を(明示的、主題的に)導入した論文とし て有名だが、僕はこれを入手できないので読んでいない。スーパーポージング 公理のオリジナル形は、Masahito Hasegawa "Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi" 1997 からの孫引きである。
一方で、Hasegawa(長谷川 真人さん)の論文(注1を参照)などでは、スーパーポージング公理を次の 形に簡略化している。
この2つはかなり異なる。ハッキリと区別するために、簡略 化されたほうを垂直タイトニング公理と呼ぶことにして、垂直タイトニング (と左右タイトニング)からもとのスーパーポージングを(定理として)導く 計算を詳しく示す。
/* superposing */
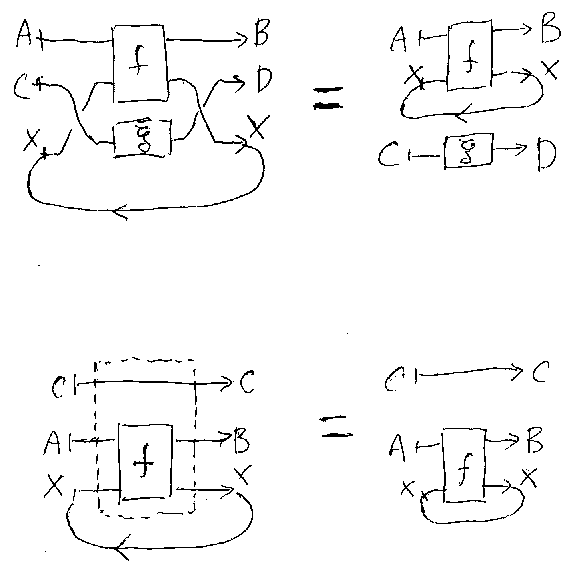
議論はすべて厳密な対称モノイド圏(symmetric strict monoidal category) のなかで行う。対称モノイド圏のモノイド積(テンソル積)を+で示す。X+Y→ Y+Xというクロス(対称)はσX,Yと書く。
射の結合(合成)は記号「;」を使い、図式順の(左から右への)結合だとす る。結合;はモノイド積+より優先度が高い演算だとする。対象Xの恒等射を 単にXと書く。ここでは、対象Xと射IdXを同じ記号で表しても問題はない (慣れないと混乱の心配はあるが)。
f:A+X→B+XのXに関するトレースはf↑XA,Bと書くが、通常はA,Bを省略 してf↑Xと書く。演算 (_)↑X は結合;よりさらに優先度が高いとする。 ただし、優先度のルールにたよらずに括弧を付けた方が分かりやすいときが多 い。
f+gを図に描くときは、fを上、gを下に描く(これは通常の習慣と逆かもしれ ない)。したがって、トレースf↑Xのループはfの下にぶらさがることにな る。図における射の向きは常に左から右である。図の描き方に関するもっと基 本的なことはETBダイアグラムを参照。
タイトニングは、トレース・ループを縮める(あるいは逆に拡げる)ときに 使う公式である。つまり、トレース作用素のスコープをより小さくする。左タ イトニングは(g+X);fという形をした被作用体(operand)をfに縮める。同様 に、右タイトニングはf;(g+X)という形をした被作用体をfに縮める。いずれも、 余分な恒等射がなくなる形をしている。
/* tightening */
簡略化されたスーパーポージング公理もやはり、トレース・ループを縮める効 果がある。つまり、C+fというトレース被作用体をfだけに縮める。恒 等射Cはなくならないが、作用スコープの外に出る。
以上の事実から、簡略化されたスーパーポージングを垂直タイトニングと呼 ぶことにする。この呼び名のほうが実情を表していると思うし、理解しやすい だろう。それに、オリジナルのスーパーポージング公理と簡略化された形を区 別して、両者を呼び分けることもできる。
トレースと直接の関係はないが、対称モノイド圏で一般に成立する事実を補 題として準備しておく。この補題は後で使う。
f:A+X→B+Yとして、(A+σC,X);(f+C);(B+σY,C) =(σA,C+X);(C+f);(σB,C+Y)
/* jump-rope */
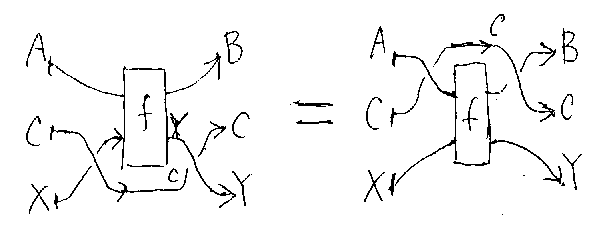
これをなぜ「縄跳びの補題」と命名したかというと、図を見ての比喩的な印 象からである。fを、AとBを両手、XとYを両足とする人だと思ってほしい。Cを 大縄だと思うと、fが縄跳びをしているように見えなくもない。縄Cは、地面か ら頭上に昇ったり、頭上から地面に降りたりしている。
縄跳びの補題を示すには、クロス(対称)σに関する次の性質が必要である。
/* cross-axioms */
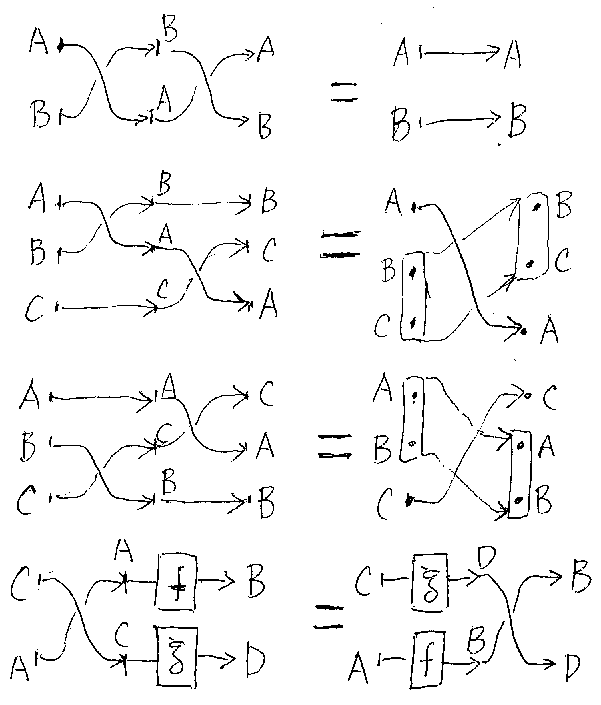
縄跳びの補題は、図で見ると自明に近いのだが、計算は意外にめんどくさい (もっと簡単な計算があるかもしれないが)。
縄跳びの補題(等式)の左辺は(A+σC,X);(f+C);(B+σY,C)だが、こ のうち、(A+σC,X);(f+C)に注目して変形しよう。変形手順は次の図に示 している。図の後に説明が続く。
/* jump-rope-calc */
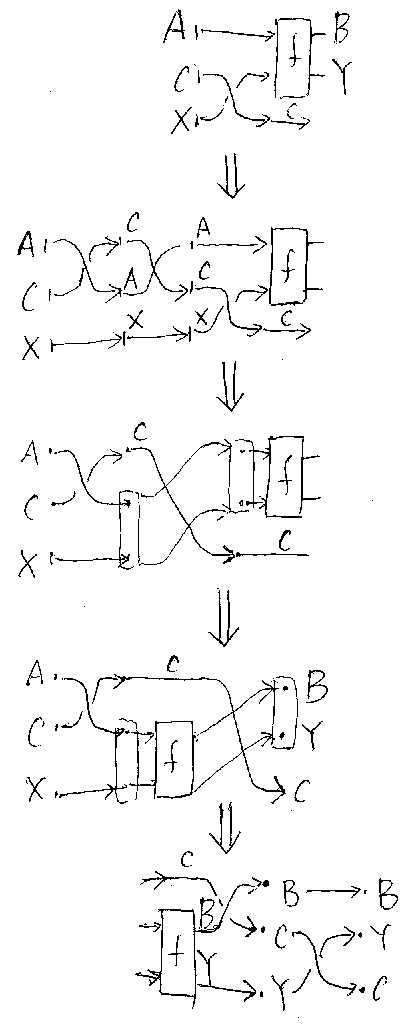
まず、(A+σC,X);(f+C) = (σA,C+X);(σC,A+X);(A+σC,X);(f+C)と変形する。ここで、 (σA,C+X);(σC,A+X) = (σA,C;σC,A)+(X;X) = (A+C)+X だ から、実は恒等射を左に結合したことになる(クロスの基本性質を思い出そう)。
次に、図の中央付近のワイヤーがからんだ部分に注目すると、 (σC,A+X);(A+σC,X)を発見できるので、これをσC,A+Xに置き換える (これも、クロスの基本性質を思い出そう)。つまり、 問題の式は、 (σA,C+X);σC,A+X;(f+C) になる。
ここで、σC,A+X;(f+C) のクロスを右に移動する(またまた、クロスの 基本性質を思い出そう)。σC,A+X;(f+C) = (C+f);σC,B+Y が適用で きるから、問題の式は、(σA,C+X);(C+f);σC,B+Y となった。
さらに、σC,B+Y を (σC,B+Y);(B+σC,Y) と分解する(これも、 クロスの基本性質!)。以上の過程をまとめれば:
この結果を利用して、縄跳びの補題の左辺を変形すれば、 (A+σC,X);(f+C);(B+σY,C) = (σA,C+X);(C+f);(σC,B+Y);(B+σC,Y);(B+σY,C) である。 だが、右にある(B+σC,Y);(B+σY,C)の部分は消えてしまう(クロス の基本性質!! 図を描いてみよ)。つまり、 (A+σC,X);(f+C);(B+σY,C) = (σA,C+X);(C+f);(σC,B+Y) だが、これは縄跳びの補題に他ならな い。
恒等射Cの代わりに一般の射g:C→Dを使っても縄飛びの補題は成立する。
(A+σC,X);(f+g);(B+σY,D)=(σA,C+X);(g+f);(σD,B+Y)
この一般形は、縄跳びの補題(特殊形)から導くこともできるし、縄跳びの 補題(特殊形)と同様にしてスクラッチから証明することもできる(練習問題 ですね)。
JSV96のオリジナルのスーパーポージング公式をわずかに簡略化して、次の形 を証明しよう。ここでは、射gを恒等射Cに限定している。
以下の図が計算過程を示している。図の後に説明が続く。
/* proof-superposing */
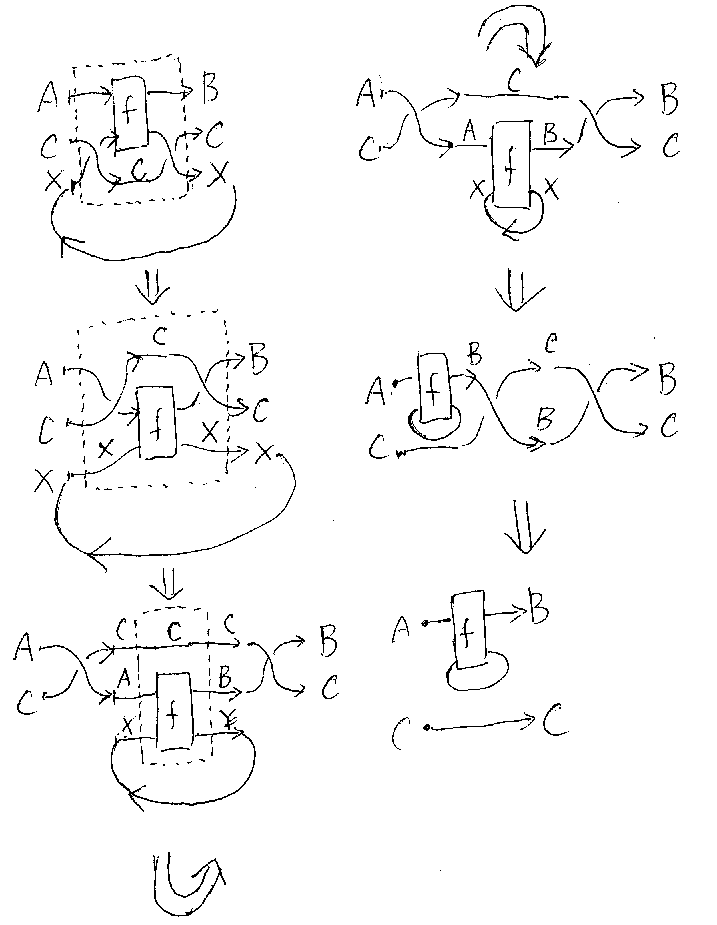
f+Cに関するスーパーポージング定理から、f+gに関するスーパーポージング 定理を導くのは簡単である。非常に基本的で頻繁に現れるテクニックを使う。こ のテクニックは、はっきりと言及しておく価値があると思うので、ここで述べ ておく。
/* shift */
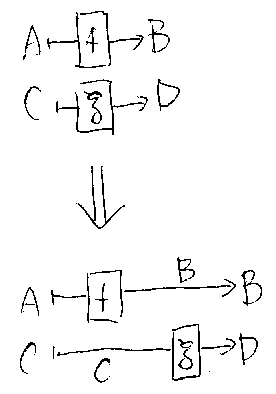
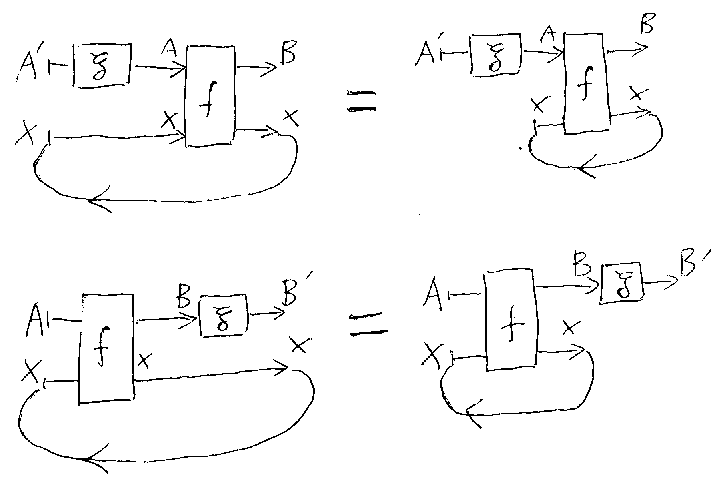
f:A→B、g:C→Dとする。f+gの絵を描くと、fとgは縦にまっすぐ並ぶ。 fとgを横方向にずらすような書き換えを考えよう。fの右側とgの左側にそれぞ れストレートワイヤー(自明なジャンクション、恒等射)を繋ぐ。こうすると、 fが左でgが右に来る。式で書けば、f+g=(f;B)+(C;g)=(f+C);(B+g)である。こ こで、f=f;Bとg=C;gは単位律だし、 (f;B)+(C;g)=(f+C);(B+g)は交替律(interchange law)である。もち ろん、ずらす方向を逆にした f+g=(A;f)+(g;D)=(A+g);(f+D)も成立する。このような操作をずらし(shift)と 呼ぶことにする(*注2)。
トレース付きモノイド圏の公理のなかに、Sliding公理がある。ずらし (shift)はこのスライディングとまぎらわしいかもしれない。だが、いい用 語が思い浮かばない。
ずらしを使えば、次の図のようにして、f+gに関するスーパーポージング定理 を示せる。
/* proof2-superposing */
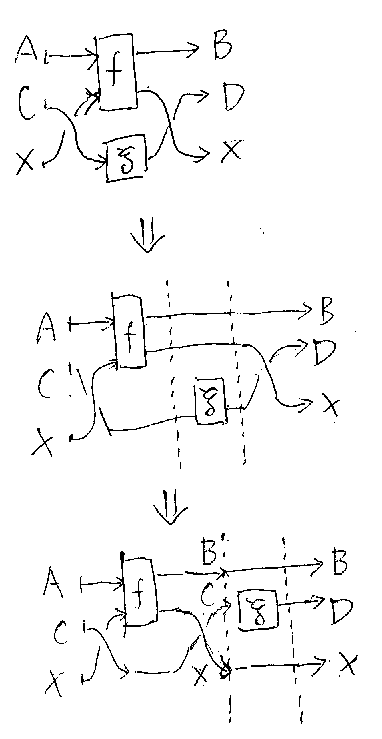
なお、縄跳びの補題の一般形を使えば、いきなりf+gのスーパーポージング定 理を示せる。が、縄跳びの補題の特殊形から一般形を導くときに、やはりずら しを使うことになる。