順序言語

檜山正幸 (HIYAMA Masayuki)
Thu Mar 10 2005:start
Fri Mar 11 2005:draft

列言語のアルファベットに順序が入っている場合に、言語にも順序構造を与 えることができる。ただし、言語の定義を少し変えたほうが都合がよい。新し い“言語の定義”のもとでも、通常の定義の場合とほとんど同じ取り扱いがで きる。

目次

1. はじめに

形式言語理論における“言語”とは、なんらかの構文的対象（語、項、文、 ツリー、グラフなど）の集合である(*注1)。それが単なる集合ではなくて、順 序構造が入っているとき、順序言語と呼ぶ(*注2)。つまり、順序言語に属する2つの 構文的対象は（部分的に）比較可能となる。

注1

では、構文的対象とは何か？ と問われると厳密な定義があるわけではない。 構文的対象と呼ばれるモノが前もってこの世に存在するわけではない。なにか を構文的な対象とみなすのは我々の主観である。つまり、ある対象を「これは 構文的対象だ」と思い、そのように取り扱えば、それは構文的対象なのである。

注2

「順序付き言語」のほうがいいかとも思った。が、"ordered xxx"の訳語は通 常「順序××」だから、その習慣に従った。

記事「折れ線の例」で述べたような問題にアプ ローチするためには、どうしても順序言語の概念が必要そうだ。そこで、この 記事で、順序言語の一般的かつ基礎的な事項について述べる。

多くの場合、アルファベット（構文的対象の基本構成素）にも ともと順序が入っていて、それにより言語（と呼ばれる集合）の上の順序構造 が定義される。よってここでは、アルファベットの順序構造から導かれた順序 だけを考える。

2. 順序付きアルファベットと、その上の列集合

Σはアルファベットとする(*注3)。Σに順序構造が入っているとき‘順序付 きアルファベット’と呼ぶ(*注4)。順序付きアルファベットは、台集合（underlying set）Σとその上の順序（partial order）≦を組にして(Σ、≦)と書くべきだ が、単にΣだけで順序も込めた集合を意味するとする。つまり、記号の乱用だ がΣ=(Σ, ≦)。

注3

文字「Σ」（シグマ）をアルファベットを表すために使うのは、形式言語理 論の習慣である。このての習慣に、たいした意味があるわけではない。にもか わわらず、従うほうが無難といえる。

注4

アンリャー、こっちでは「順序付き」になっている。無意識だった、気が付 かなかった。直したほうがいいかな？

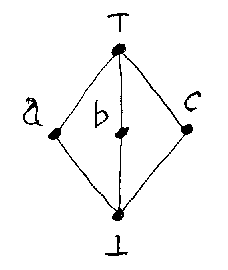
次の図は、順序付きアルファベットの例である。

FIG: 順序付きアルファベットの例

/* ordered-alphabet */

Σのメンバーから構成される列の全体をSeq(Σ)とする。Seq(Σ)のメンバー、 つまり列をα、βなどで表す。1以上の整数iに対して、αiは、列αのi番目 に出現するΣのメンバーだとする(*注5)。

注5

インデックス番号を0からはじめるか、1からはじめるかは、いつでも悩んで しまうが、この記事では1からの番号付けとする。

Σに順序が定義されていれば、Seq(Σ)にも順序が入る。その定義は以下のと おり。

α, β∈Seq(Σ)だとして、α≦βとは：

  1. length(α) = length(β)
  2. 1 ≦ i ≦ length(α)であるすべての整数iに関して、αi≦βi

Σを上の図のような順序が入った集合{a, b, c, T, ⊥}だとして、いくつか の例を挙げる。

  1. "abc"と"ab"は比較不能（長さが違うので）
  2. "abc"≦"abT"
  3. "a⊥c"≦"abT"
  4. "abc"≦"TTT"

列の順序の定義から、length(α)≠length(β) なら、 αとβは比較不能である。よって、すべての列ξに対してξ≦αとなるよ うなα（つまり、最大元）は存在しない。同様に最小元も存在しない。ただし、 長さnの列のなかでの最大元／最小元は存在するかもしれない(*注6)。

注6

すべての列に対する最大元／最小元が存在するように、定義を手直しするこ とは容易であるが、今は必要がないから考えないことにする。

Σが順序集合のとき、Seq(Σ)も上の定義で順序集合になる。つまり、Seq(Σ) 上に定義された≦は次を満たす。（定義からただちに従う。）

  1. α≦α
  2. α≦β、β≦γならば、α≦γ
  3. α≦β、β≦αならば、α=β

列の連接（concatenation）に関して、次が成立する(*注7)。これらの性 質も、≦の定義に沿えば容易に確認できる（練習問題）。

  1. α≦βならばαγ≦βγ
  2. α≦βならばγα≦γβ
注7

つまり、Seq(Σ)は、連接に関して順序モノイドとなる。

3. 下方閉な部分集合

ここで、後で使う都合から、順序集合の一般論を少し議論しておく。

順序集合Xの部分集合Aが次の条件を満たすとき、‘下方閉’（lower closed） という。

全体集合Xと空集合Oは明らかに下方閉である。A、Bが下方閉だとすると、次 が成立する。

  1. A∪Bは下方閉である。
  2. A∩Bは下方閉である。

1番目を示してみよう。

より一般に、{Ai | i∈I} が下方閉な集合Ai達の族だとして、次が言え る：

  1. ∪iAiは下方閉である。
  2. ∩iAiは下方閉である。

今度は2番目だけ示してみる。

Pow(X)はXの部分集合全体の集合（ベキ集合）、PowLC(X)を、Xの下方閉 部分集合の全体とする。PowLC(X) ⊆ Pow(X) である。 今述べたPowLC(X)の性質から、Pow(X)の束演算をPowLC(X)に制限でき る。この制限した演算により、 PowLC(X)は集合束になる。

4. 言語の定義

第2節で、アルファベットΣが順序集合なら、Seq(Σ)も順序集合 にできることがわかった。このとき、Σのメンバーを長さ1の列として埋め込 む写像 Σ→Seq(Σ)は、順序を保つ写像になっている。また、Seq(Σ)上で連 接演算を考えると、順序モノイドになるのだった。

さて、通常の形式言語の定義では、Seq(Σ)の任意の部分集合を言語と呼ぶのだが、 この定義をそのまま採用するのは良くない。単なるSeq(Σ)の部分集合を言語 だとすると、話がなめらかに進まない。条件を付けることにする。

順序付きアルファベット上の言語は、次のように定義する。

言語は、（順序集合と考えた）Seq(Σ)の部分集合だから、Seq(Σ)から誘導 された順序を持つ。つまり、上で定義した言語は順序言語である。

なお、Σに順序がないとき、“離散順序がある”とみなしてΣを（特別な） 順序集合と考えることができる。（離散順序とは、「x≦y ⇔ x=y」として定 義される順序である。）そのとき、上の“言語の定義”は通常の“言語の定義” に一致する。なぜなら、Seq(Σ)も離散順序集合になるので、任意の部分集合 が下方閉となるからである。

順序付きアルファベットΣから生成される言語の全体をLang(Σ)とする。 Lang(Σ) = PowLC(Seq(Σ)) である。第3節の結果から、 Lang(Σ)は集合束になる。

AとBが言語のとき、ABはAとBの連接言語だとする。‘言語の連接’の定義は 次のとおり。

“言語”の定義より、AもBも下方閉であるが、ABが下方閉であることを示さ ないと、上の定義はwell-definedではない。ABが下方閉であることは次のよう に示せる： ABのメンバーは、α∈Aとβ∈Bを使ってαβの形に書ける。γ≦ αβだとして、このγがABのメンバーになることを示せばよい。≦の定義より、 γ≦αβであるならγとαβは長さが等しい。γを“αと同じ長さの前半”と “βと同じ長さの後半”に分けて、γ=γ1γ2と書く。すると、γ1≦α、 γ2≦βとなるが、AとBが下方閉だったから、γ1∈A、γ2∈B。つまり、 γは、γ1∈A、γ2∈Bであるγ1、γ2によりγ=γ1γ2と書ける のだから、ABのメンバーである。

ここで、「α1とβ1が同じ長さ、α2とβ2が同じ長さのとき、 α1α2≦β1β2ならば、α1≦α2、かつβ1≦β2」という性 質を使っている。これも≦の定義からすぐ出る性質である。

これで、Lang(Σ)は、集合束であると同時にモノイドであることが分かった。 さらに、∪に関しては次の分配法則が成立する。

  1. A（∪iBi） = ∪i(ABi)
  2. (∪iAi)B = ∪i(AiB)

1番目の等式で、まず A（∪iBi）⊆ ∪i(ABi) を示そう。 A（∪iBi）のメンバーは、α∈Aとβ∈∪iBiによりαβと書ける。と ころでβ∈∪iBiとは、適当なk∈Iがあってβ∈Bkのことであるから、 αβ∈ABk、よって、αβ∈∪i(ABi)。

次に、逆向きの ∪i(ABi) ⊆ A（∪iBi）を示そう。∪i(ABi)の メンバーは、適当なk∈Iに対してABkのメンバーである。つまり、α∈Aとβ ∈Bkによりαβと書ける。β∈Bkなら当然にβ∈∪iBiだから、 αβ∈A(∪iBi)。

2番目も同様に示せる。

∩に関しては、A(B∩C) = AB∩AC さえ成立しない。 例えば、A={ε, a}、B= {ε, a} C={aa}とすると：

A(B∩C) = BO = O （空）
AB∩AC = {ε, a, aa}∩{aa, aaa} = {aa}

だが、A(B∩C) ⊆ AB∩AC は成立する（練習問題）。

5. 正規表現

この節では、正規表現とその解釈を与える。正規表現の構文は通常とまった く同じであるが、解釈は少し変わる。

最初に、正規表現を形式的な項として定義する。形式的な定義に関しては、 記事「『形式的』とは何だろう」を参照。使う 演算記号（関数記号）は、「;」、「|」、「*」であり、それぞれ、連接、合 併、Kleeneスターを表す心積もりである。

正規表現は次のように帰納的（inductive）に定義される。

  1. 定数記号0、1は正規表現である。
  2. Σのメンバーは正規表現である。
  3. r, sが正規表現のとき、(r;s)は正規表現である。
  4. r, sが正規表現のとき、(r | s)は正規表現である。
  5. rが正規表現のとき、(r*)は正規表現である。
  6. 以上の手順で得られるものだけが正規表現である。

例えば、a, b, c∈Σだとして、(((1 | a);b) | (b;(c*))) は正規表現であ る。余分な丸括弧を省略して、演算子の優先順位は、*、;、|の順で優先され ると決めれば、(1 | a);b | b;c* と簡略化できる。以下では、 適宜簡略な表現を用いることにする。

正規表現の解釈を示すために、いくつかの約束をする。

  1. x∈Σに対して、xだけからなる長さ1の列を[x]と書くことにする。 通常は、xと[x]を区別しないが、ここでは区別する。
  2. α∈Seq(Σ)に対して、α↓ = {β∈Seq(Σ) | β≦α}としてα↓を定義 する。α↓は、Seq(Σ)の下方閉な部分集合になる。従って、α↓は言語 である。

εは空列として、ε↓ = {β∈Seq(Σ) | β≦ε}は{ε}である。なぜなら、 β≦εであるためには、βは長さが0でなくてはならないが、長さ0の列はε以 外にないから。

正規表現rに対して、その意味（値）をM(r)と書くことにする。 どんな正規表現rに対してもM(r)は言語である。

  1. M(0) = {}（空言語）、M(1) = {ε}。
  2. a∈Σだとして、M(a) = [a]↓。
  3. M(r;s) = M(r)M(s) （連接言語）。
  4. M(r | s) = M(r)∪M(s)
  5. M(r*) = M(r)*

最後のM(r)*だけは説明を補足しておく。任意の言語A（Seq(Σ)の下方閉な 部分集合）に対して、A* = {ε}∪A∪AA∪AAA∪ ... である。 これは、A0 = {ε}、A1 = A、A2 = AA、… として、A* = ∪iAi （i=0, 1, 2, ...）とも書ける。各Aiは下方閉だから、それらの合併も下方 閉である。よって、 A* も下方閉である。

定義に従ってM((1 | a);b | b;c*)を計算してみる。ただし、[a]↓=A、[b]↓=B、 [c]↓=Cとする。

M((1 | a);b | b;c*)
= M((1 | a);b)∪M(b;c*)
= (M(1 | a)M(b))∪M(b)M(c*)
= (M(1)∪M(a))M(b)∪M(b)M(c)*
= ({ε}∪A)B∪BC*

({ε}∪A)B∪BC* をさらに計算すると：

({ε}∪A)B∪BC*
= {ε}B∪AB∪BC*
= B∪AB∪BC*
= AB∪BC* (B⊆BC*だから)

6. おわりに

順序付きアルファベットから生成される順序言語（の族）も、通常の言語と それほど異ならないことがわかった。実際、順序を考慮しても、負担が極端に 増えることはない。一方、順序言語を導入することにより明らかになる現象は けっこう多い。その意味で、順序言語は“お得な”概念である。

応用例は別な記事で述べるが、記事「折れ線の例」 で提示した問題を解くことは、1つの応用例になる。