/* cross-axioms */
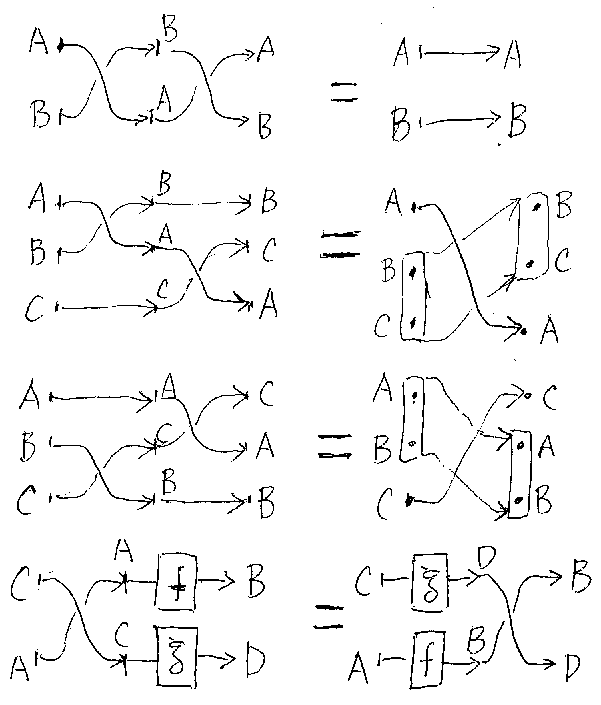
まず、対称モノイド圏に双対オペレータを導入し、そうして得られた双対付 き対称モノイド圏に、180度回転する“曲がった射”であるKelly単位を加えて コンパクト閉圏を定義する。これは、従来の定義に比べ冗長だが、計算や図解 は容易になる。
記事「コンパクト閉圏」の第3章の終 わりに次のように書いた。
コンパクト閉圏を使う側としては、基本的な性質は最初から列挙されていたほ うがいい。Kelly & Laplazaの定義は、公理の最小化を重視しているようだが、 冗長でも、もっと計算に便利な定式化があったほうがいいと僕は思う。
というわけで、実際に、より使いやすい「コンパクト閉圏の定義」を考えて みた。公理を最小化することはまったく度外視して、計算や図解に便利な性質 は最初から(冗長であっても)定義に含めてしまう方針である(*注1)。この方針を採 用すると、コンパクト閉圏に至る手前で双対付き対称モノイド圏(symmetric monoidal category with dualizer)という概念が登場する。
このような定義の欠点/問題点は、公理が多くなるので、ある圏がコンパク ト閉圏であることを確かめるのに手間がかかってしまうことだ。公理が最 小化されていれば、確認の手間も最小で済む。
双対付き対称モノイド圏は自然な概念で、それ自身(コンパクト閉圏と無関 係な文脈)でも意味を持ちそうだ。この双対付き対称モノイド圏に、単位 (unit)を導入してコンパクト閉圏を定義する。問題は、単位の性質をどのよ うに規定するかである。結果的には、「単位ηと対称性σ」、 「単位ηと双対*」、「単位ηとモノイド演算+」とのそれぞれの関係を述べる 3つの等式を公理とした。
以下では、圏Cの対象は|C|で表す。A∈|C|に対して、Aの恒等射(identity, ストレート・ジャンクション)をιAで表す。 また、混乱がなければιAを単にAとも書く。なお本記事では、定義の条件な どを等号を使って述べる。つまり、厳密(strict)なケースだけを考えている。
(C; +, 0, σ)を対称モノイド圏(symmetric monoidal category)とする。+ はモノイド演算(monoidal operation)、0はモノイド単位(monoidal unit)、 σA,B:A+B → B+A は、対称性を与える射(クロ ス・ジャンクション)だとする。σに関しては次を仮定する。
/* cross-axioms */
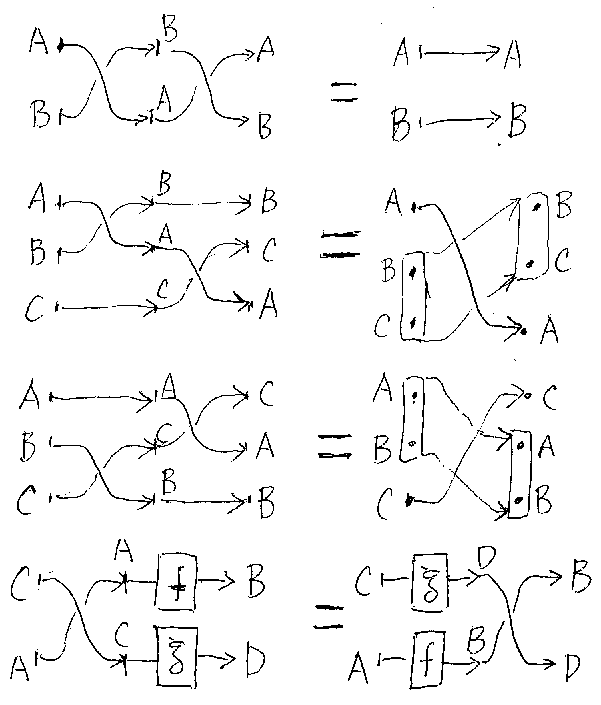
(C;+ , 0, σ)と(D;+ , 0, σ)が2つの対称モノイド圏とすると、関手F:C→D が次を満たすとき、‘対称モノイド関手’と呼ぶ(*注2)。
対称モノイド関手の定義はいくつかありえる。ここに挙げた定義は、おそら く一番きびしい(強い条件を要求する)ものである。
反変の対称モノイド関手も同様に定義できる。対称モノイド圏C上の反変対称 モノイド自己関手F:C→C が F;F=IdC であるとき、Fを‘双対オペレータ’ (dualizing operator, dualizer)と呼ぶ。Fが双対オペレータのとき、F(A)、 F(f)の代わりにA*、f*のように書く。双対オペレータの性質をすべて列挙 すれば、次のとおり。
双対オペレータが備わった対称モノイド圏を‘双対付き対称モノイド圏’ (symmetric monoidal category with dualizer)と呼び、(C;+, 0, σ, *)の ように書く。
A∈|A|に対してηAは、コンパクト閉圏の単位だとする。モノイド単位や随 伴関手の単位と混同しないように、以下では‘Kelly単位’と呼ぶことにする。 Kelly単位は、「お絵描き圏論」の第6節 で「ターニング・ジャンクション」と呼んだものであり、半円形のカーブとし て描かれる(*注3)。Kelly単位の特徴付けこそがコンパクト閉圏定義の本質的 な部分となる。
カーブとしての図示が多いが、Abramskyは三角形で描いている。三角形のほ うが図のレイアウトをしやすいメリットがある。また、カーブで描くと、 Kelly単位=ターニング・ジャンクションが射であることを忘れがちなので、 その点でも三角形はいいかもしれない。
オリジナル(Kelly & Laplaza)の定義では、ηA:0→A*+A とは別に Kelly余単位 εA:A+A* → 0 の存在が仮定され、次の「Z字引き伸ばし」と「S字引き伸ばし 」の等式が成立することがコンパクト閉圏の条件となっている(*注4)。 (これらの等式は、三角恒等式、ジグザグ恒等式、剛性(rigid)公理などと 呼ばれる。)
もっとも、Kelly & Laplazaは入手できないので、「オリジナルの定義」のオリ ジナルは確認してない。
/* turning-stretching */
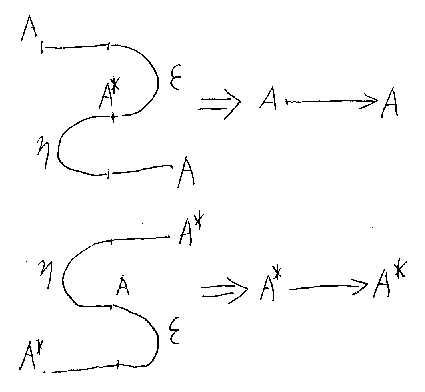
我々の設定では、最初から双対オペレータ(dualizing operator、dualizer) の存在を仮定しているので、ηだけあれば、εは εA = (ηA)* として 定義できる。例えば、Z字引き延ばしは、ηだけを使って (A + ηA);((ηA)* + A) = A と書ける。だが、便利なので記号εも使 うことにする。その他に次の定義をする。
さて、Kelly単位ηを規定するために選んだ条件は次の3つである。後に続く 節でそれぞれを説明する。
双対付き対称モノイド圏(C; +, 0, σ)に、これらの等式を満たす η = {ηA | A∈|C| }を加えた構造(C; +, 0, σ, η)が‘コンパクト閉圏’ である。
ねじり公式を導入した直接の動機は、(トレース付きモノイド圏の)ヤンキ ング公理を示すときに必要だからだが、 Abramsky の強コンパクト閉圏(Peter Selingerによれば、ダガー・コンパクト閉圏)でも同様な仮定を置いてい たのも採用の理由である(*注5)。
ηA;σA*,A = ηA* の両辺に*(双対化)を作用させると、 (σA*,A)*;(ηA)* = (ηA*)* となり、 σA,A*;εA = εA* = ε'A が得られる。念のため、もとのね じり公式と今得られた双対版を並べて書いておく。
ダガー・コンパクト閉圏におけるねじり公式の類似は、ダガー演算†を使っ て次のように書ける。
ねじり公式の意味するところは次の図のように単純である。
/* twisting */
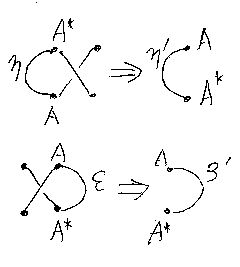
応用例として、ねじり公式とS字引き伸ばし公式の一種を仮定して、ヤンキン グ(yanking)公理を示してみよう(説明は図の後)。
/* yanking-in-ccc */
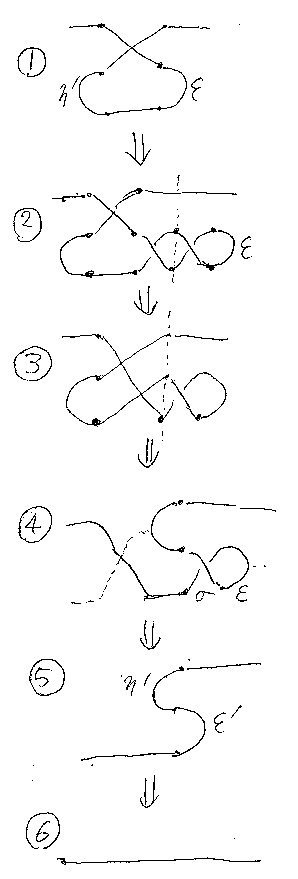
我々は、双対付き対称モノイド圏から出発しているので、最初から双対オペ レータが備わっている。しかし、オリジナル(Kelly & Laplaza)のコンパク ト閉圏の定義では、射の双対は対象の双対とKelly単位を使って組み立てられ る。この食い違いを埋めるために、最初から存在する双対オペレータが、 Kelly/Laplaza流の“定義された双対”に一致することを仮定する。それが、 次の双対化公式である。
公理として仮定する双対化公式は1つでよいが、その変種を導いておく(下の 図も参照)。まず、ねじり公式を少し変形すると、次が得られる(これもねじ り公式と呼ぶ)。
双対化公式のηとεをねじったもので置き換えると、左辺が (η'A;σA,A* + B*);(A* + f + B*);(A* + σB,B*;ε'B) となるが、ク ロスの性質を使って2個のねじれを相殺すると(各自、図を描け)、(B* + η'A);(B* + f + A*);(ε'A + A*)が得られるが、これもf* の表示になっている。よって次が成立する。
一方、双対化公式の両辺の双対を取り、ε = η*、η = ε* に注意すれ ば次が得られる。
バランスを考えれば、もう1つの公式があることは分かるだろう。4番目の双 対化公式の図示と導出は練習問題とする(実は、図を描き間違えたので4番目 を削除した、というのがホントの事情)。
/* dualizing */
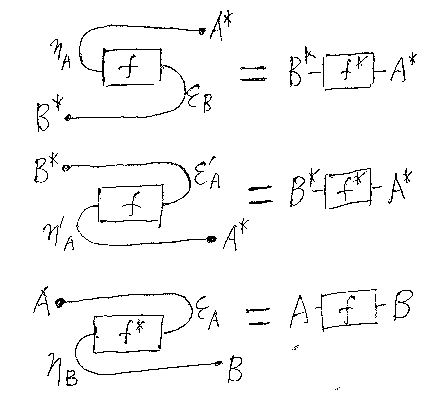
ねじり公式は、ηA とηA*の関係を記述している。また、0* = 0 と 0 + 0 = 0 を使えばη0 = 0 も分かる。もし、ηA + BをηAとηB で書き下す公式があるならば、双対付きモノイド(|C|, +, 0, *)上で定義され た変換η(*注6)の性質が明白になる。まとめ公式は、ηA + Bを、ηA とηB、それと基本演算(;、+、*)で与えるものである。
CとDが圏だとして、α:|C|→Mor(D)の形の写像を変換と呼ぶ。Mor(D)はDの射 で、A∈|C|に対してα(A):dom(α(A))→cod(α(A))となる。関手F, G:C→Dに 対して、dom(α(A)) = F(A)、cod(α(A))=G(A) で適当な条件を満たすとき、F からGへの自然変換になる。自然変換以外にも、対称で添字付けられた射の族 は出現する。
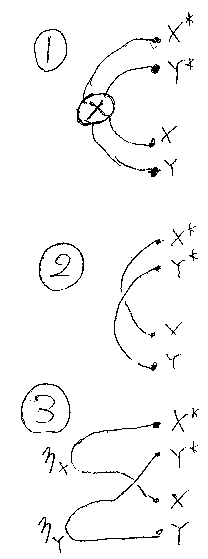
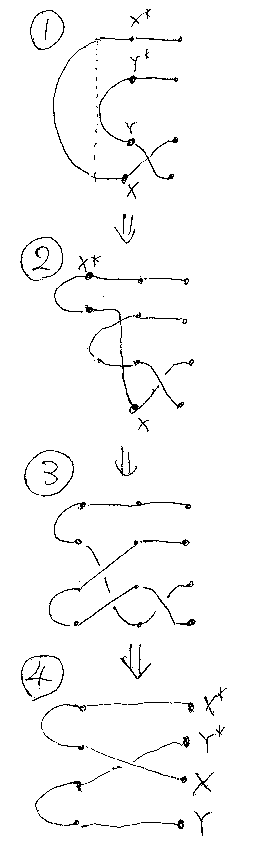
以下にこの公式の背景を説明しよう。X* + Y* から X + Y へと、カーブ したワイヤーで繋ごうと思うと、ストレートワイヤーでは無理で、曲がりと共 にねじりを入れる必要がある。つまり、ターニング・ジャンクションはリバー ス・ケーブルなのである(下図の1番)。リバース(クロス)・ケーブルをばらすと、交差 した2本のケーブルになる(下図の2番)。交差とつながりの具合を記述すると、 まとめ公式の左辺になる(下図の3番)。(等式ではA, B、図ではX, Yとなっ ているのは手違い。直さないけどカンベンしてね。)
/* bundling */
コンパクト閉圏の通常の定義では、S字とZ字の引き伸ばし公式であるジグザ グ恒等式(三角恒等式、剛性公理)がアプリオリに仮定される。我々の定義で は、ジグザグ恒等式は双対化公式の特殊ケースとして得られる。
双対化公式 (A + ηB);(A + f* + B);(εA + B) = fにおけるfを、A = ιA:A→Aと置くと、 (A + ηA);(A + A* + A);(εA + A) = A となる。 (A + A* + A)は省略していいので、(A + ηA);(εA + A) = A だが、こ れはZ字の引き伸ばし公式に他ならない。S字の引き伸ばしも同様に得られる。
双対化公式とジグザグ恒等式を用いて、トレース付きモノイド圏のスライディ ング公理を簡略化した形を示そう。スライディング公理と比べて、スライディ ングと回転の量が半分なので、仮に半スライディング公式と呼んでおこう。
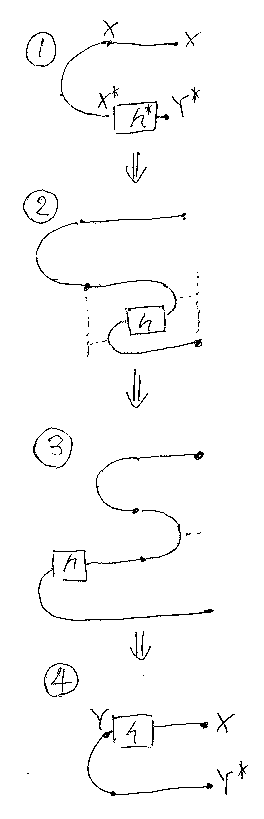
半スライディング公式は、h:Y→Xに対して次の形をしている。
これは、h* をターニング・ジャンクションのカーブに沿って移動(スライ ド)させると、カーブの曲がりの影響を受けて180度ひっくり返ることを意味 する。h* がひっくり返ると h になる。双対の定義と引き伸ばしを使って次 のように示せる(説明は図の後)。
/* sliding-in-ccc */
スライディング公理の場合と同じように、トレース付きモノイド圏のバニッ シング公理の“半分バージョン”がコンパクト閉圏で成立する。これを、半バ ニッシング公式と呼ぶことにする。次のものである。
まとめ公式を考慮に入れると、次の形でも同じである。
この半バニッシング公式を示すための補題として、 (ηX + Y) = (Y + ηX)(σY,X* + X)(X* + σY,X) を示す(下図)。 これは、ターニング・ジャンクションとストレート・ジャンクションの並列が あったとき、ターニングと2回交差する形で順序交換をしていいこと、その逆 に2回の交差を解消していいことを主張している。仮にクロスオーバー公式と 呼んでおこう。
/* crossing-over0 */
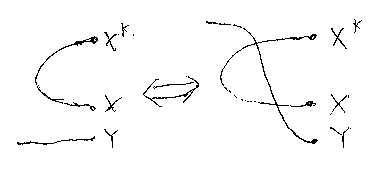
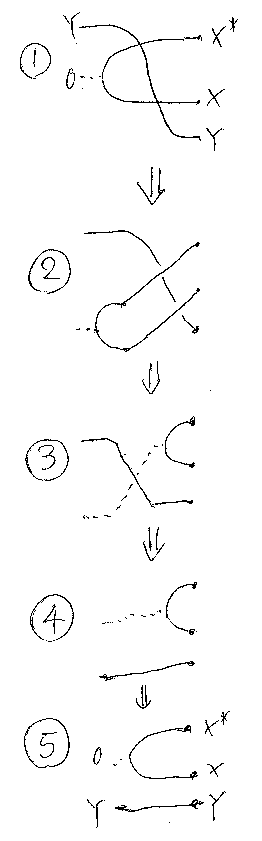
2回の交差を解消する方向に変形して示すことにする(説明は図の後)。
/* crossing-over */
このクロスオーバー公式を使うと、半バニッシング公式を次のように示すこ とができる(詳細は練習問題)。
/* vanishing-in-ccc */
「お絵描き圏論」でも述べたように、ηA、η'A、εA、ε'A は、半 円形のカーブ、または180度の回転を与えるものである。一方、双対オペレー タも射を逆さまにする操作なので、ηと無関係であるはずがない。 コンパク ト閉圏を定義する等式群は、これら、入れ替え、鏡映、ねじれ、回転などの 「逆さまにする/ひっくり返す」操作の相互関係を規定したものである。「逆さま/ひっくり返し」の導入に より、通常の圏では不可能だったルーピングが導入され、再帰や繰り返しの記 述にも使えるようになった。
コンパクト閉圏と密接な関係を持つトレース付きモノイド圏は、反対の極性 を持つ対象や射(鏡の世界の存在、反物質?)が露骨に出現しないように工夫 された世界である。負(極性が通常とは反対)のモノは、トレース演算にうま く隠されて(閉じこめられて)表には顔を出さないようになっている。コンパ クト閉圏では、トレース付きモノイド圏で成立する法則の“半分バージョン” が成立するが、これは i×i = -1 のようなもので、実世界での逆さま操作が、 鏡の世界の半分操作2つで実現されている、ということだろう。実際トレース は、180度回転であるターニングジャンクション(Kelly単位)を2つ繋げて実 現される。